
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЛЕКЦІЯ 21. ЧИСЛОВИЙ РЯД, ОСНОВНІ ОЗНАЧЕННЯ.НЕОБХІДНА УМОВА ЗБІЖНОСТІ. ДІЇ З РЯДАМИ. РЯДИ З ДОДАТНИМИ ЧЛЕНАМИ ТА ЇХ ВЛАСТИВОСТІВизначення числового ряду. Сума ряду Означення. Нехай дана нескінченна послідовність чисел
Означення. Сума скінченого числа n перших членів ряду називається n-ою частковою сумою ряду:
Розглянемо часткові суми Означення. Якщо існує кінцева границя Приклад. Розглянемо ряд
Це геометрична прогресія з першим членом а і знаменником q Сума n перших членів геометричної прогресії дорівнює (при
Якщо Якщо
Теорема. Геометричний ряд збігається при Властивості числових рядів із додатними членами Теорема 1. Якщо до ряду (21.1) додати або відняти кінцеве число членів ряду, то отриманий ряд збігається або розбігається одночасно з рядом (21.1). Теорема 2. Сталий множник виноситься за знак суми ряду: Теорема 3. Два збіжні ряди можна почленно складати і їх сума дорівнює: Теорема 4. Сума (різниця) збіжного ряду і розбіжного є розбіжний ряд. Необхідна ознака збіжності ряду Теорема. Якщо ряд збігається, то його n-й член прямує до нуля при необмеженому зростанні n. Доказ. Нехай ряд 
Але Отже, Зауваження. Якщо Приклад. Ряд Приклад. Розглянемо ряд Тут Для доведення замінимо деякі члени ряду меншими числами і переконаємося, що навіть сума менших доданків буде прагнути до нескінченності. Випишемо декілька перших членів гармонічного ряду, розбивши їх на групи таким чином:
У кожній із круглих дужок замінимо усі доданки останнім, який залишимо без зміни. Одержимо (під кожній дужкою підписане число доданків у ній)
Із сказаного ясно, що часткові суми гармонічного ряду будуть нескінченно зростати, отже, ряд розбігається. ЛЕКЦІЯ 22. ДОСТАТНІ ОЗНАКИ ЗБІЖНОСТІ: ПОРІВНЯЛЬНА, ДАЛАМБЕРА, РАДИКАЛЬНА. ІНТЕГРАЛЬНА ОЗНАКА КОШІ Ознака порівняння Ознака порівняння. Нехай дані два ряди з невід'ємними членами 1) Якщо збігається ряд (22.2), то збігається і ряд (22.1). 2) Якщо розбігається ряд (22.1), то розбігається і ряд (22.2). Для порівняння часто використовують ряди:
Приклад. Дослідити на збіжність ряд Розв'язок. Члени даного ряду менше відповідних членів ряду Приклад. Дослідити на збіжність ряд Розв'язок. Порівняємо даний ряд із рядом |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 355. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Вираз
Вираз (21.1)
(21.1) - загальний член ряду.
- загальний член ряду. .
. ,
,  ,
,  ,…,
,…, 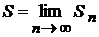 , то її називають сумою ряду (21.1) і говорять, що ряд збігається. Якщо
, то її називають сумою ряду (21.1) і говорять, що ряд збігається. Якщо  не існує, то говорять, що ряд (21.1) розбігається і суми не має.
не існує, то говорять, що ряд (21.1) розбігається і суми не має. (21.2)
(21.2) .
. ):
):

 , то ряд (21.2) має вигляд
, то ряд (21.2) має вигляд  У цьому випадку
У цьому випадку  ,
,  , ряд розбігається.
, ряд розбігається. , то ряд (21.2) має вигляд
, то ряд (21.2) має вигляд  У цьому випадку
У цьому випадку
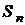 границі не має - ряд розбігається.
границі не має - ряд розбігається. і розбігається при
і розбігається при  .
. .
. .
. збігається, тобто має місце рівність
збігається, тобто має місце рівність  , де S - сума ряду; то тоді має місце також рівність
, де S - сума ряду; то тоді має місце також рівність 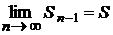 , тому що при
, тому що при 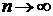 і
і  . Віднімаючи почленно з першої рівності другу, получимо
. Віднімаючи почленно з першої рівності другу, получимо
 .
. .
. , що і було потрібно довести.
, що і було потрібно довести. , то ряд розбіжний.
, то ряд розбіжний. розбіжний, тому що
розбіжний, тому що .
. , який називається гармонічним.
, який називається гармонічним.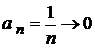 , але проте ряд розбігається. Справді, зараз ми доведемо, що
, але проте ряд розбігається. Справді, зараз ми доведемо, що  при
при 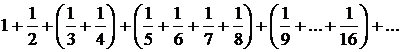

 . Оскільки таких дужок можна брати скільки завгодно, сума їх буде прагнути до нескінченності.
. Оскільки таких дужок можна брати скільки завгодно, сума їх буде прагнути до нескінченності. (22.1) і
(22.1) і  (22.2) і нехай кожний член ряду (22.1) не більше відповідного члена ряду (22.2), тобто
(22.2) і нехай кожний член ряду (22.1) не більше відповідного члена ряду (22.2), тобто 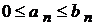
 . Тоді:
. Тоді: ,
, 

 .
.  . Так як ряд
. Так як ряд 
 . Тому що
. Тому що  і ряд
і ряд