
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод інтегрування частинамиСтр 1 из 10Следующая ⇒ НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ ЛЕКЦІЯ 12. ПОНЯТТЯ ПЕРВІСНОЇ ТА НЕВИЗНАЧЕНОГО ІНТЕГРАЛА. ВЛАСТИВОСТІ НЕВИЗНАЧЕНОГО ІНТЕГРАЛА. ТАБЛИЦЯ ОСНОВНИХ ФОРМУЛ ІНТЕГРУВАННЯ Первісна функція і невизначений інтеграл Займаючись диференціюванням функцій, ми ставили перед собою таку задачу: по даній функції знайти її похідну. Тепер перейдемо до вивчення оберненої задачі: знайти функцію, знаючи її похідну. Означення. Функція Якщо функція Означення. Невизначеним інтегралом від функції Знаходження невизначеного інтеграла називається інтегруванням функції. Властивості невизначеного інтеграла 1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції, тобто, якщо
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу
3. Невизначений інтеграл від диференціала деякої функції дорівнює цієї функції плюс довільна стала
4. Невизначений інтеграл від алгебраїчної суми двох або декількох функцій дорівнює алгебраїчній сумі інтегралів:
5. Постійний множник можна виносити за знак інтеграла, тобто, якщо
6. Якщо
Таблиця інтегралів

ЛЕКЦІЯ 13. МЕТОДИ ІНТЕГРУВАННЯ Безпосереднє інтегрування Безпосереднім інтегруванням будемо називати інтегрування за допомогою властивостей невизначеного інтеграла, тотожних перетворень підінтегральної функції і таблиці основних інтегралів. Приклад. Приклад.
Приклад. Використавши властивість № 6 знайти Приклад. Приклад. Інтегрування методом заміни змінної Заміна змінної в невизначеному інтегралі проводиться за допомогою підстановок двох видів: 1)
2)
Приклад. Приклад. Приклад. Приклад. Метод інтегрування частинами Нехай
Маємо
Ця формула називається формулою інтегрування частинами. За допомогою цієї формули знаходження інтеграла При цьому за u береться така функція, яка при диференціюванні спрощується, а за dv - та частина підінтегрального виразу, інтеграл від якої відомий або може бути знайдений. Класи інтегралів, що інтегруються частинами: Приклад.
Приклад.
Приклад. Приклад. Проінтегрувавши частинами ще раз маємо
Після двократного інтегрування частинами, ми в правій частині знову одержали початковий інтеграл. Таким чином, приходимо до рівняння з невідомим інтегралом. З цього рівняння знаходимо
ВИЗНАЧЕНИЙ ІНТЕГРАЛ Формула Ньютона - Лейбніца
де Приклад. Обчислити визначений інтеграл: |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 356. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 називається первісною для функції
називається первісною для функції  для
для  , якщо у всіх точках
, якщо у всіх точках  виконується рівність
виконується рівність  .
. , де С - деяке дійсне число.
, де С - деяке дійсне число.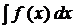 . Таким чином, за означенням,
. Таким чином, за означенням,  , якщо
, якщо  - підінтегральним виразом, знак
- підінтегральним виразом, знак  - знаком інтеграла.
- знаком інтеграла.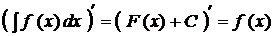 .
. .
. .
. .
. , то
, то .
. .
.




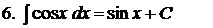

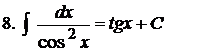

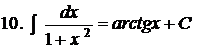



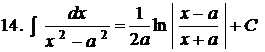
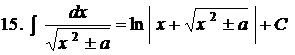



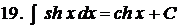
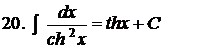

 .
.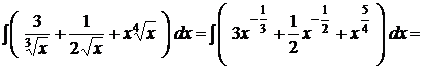
 .
. .
.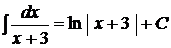 .
. .
. , де
, де 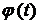 - монотонна, неперервно диференційовна функція нової змінної t. Тоді
- монотонна, неперервно диференційовна функція нової змінної t. Тоді  . Формула заміни змінної в цьому випадку має вид
. Формула заміни змінної в цьому випадку має вид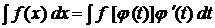 .
.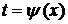 , де t - нова змінна. Формула заміни змінної при такій підстановці має вид
, де t - нова змінна. Формула заміни змінної при такій підстановці має вид .
.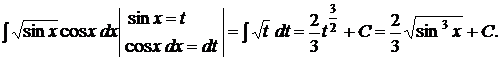
 .
.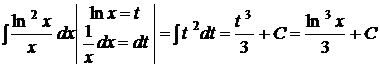 .
. .
. і
і  - дві неперервно диференційовані функції від х. Тоді використавши формулу для диференціала добутку
- дві неперервно диференційовані функції від х. Тоді використавши формулу для диференціала добутку  :
: .
. або
або . (1)
. (1) зводиться до знаходження іншого інтеграла
зводиться до знаходження іншого інтеграла  ; її застосування доцільно в тих випадках, коли останній інтеграл або простіше вихідного, або йому подібний.
; її застосування доцільно в тих випадках, коли останній інтеграл або простіше вихідного, або йому подібний. ,
, 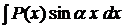 ,
,  , де
, де 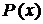 - многочлен, за u слід прийняти
- многочлен, за u слід прийняти  ,
,  ,
,  ; для інтегралів виду
; для інтегралів виду  ,
,  ,
,  ,
,  ,
,  за u приймаються відповідно функції
за u приймаються відповідно функції 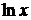 ,
,  ,
,  ,
, 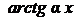 ,
,  , а за dv - вираз
, а за dv - вираз  .
.
 .
.
 .
.

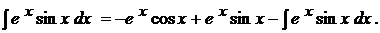
 тобто
тобто
 , (2)
, (2) - первісна функції
- первісна функції  або невизначений інтеграл.
або невизначений інтеграл. .
.