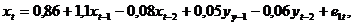Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения с распределённым лагом (лаги Алмон)
Если в правой части уравнения присутствует только независимая переменная со своими лаговыми значениями, то такое уравнение называется уравнением с распределённым лагом. Если максимальная величина лага ограничена (например, величиной l), то такое уравнение можно записать в виде В общем случае оценить параметры такого уравнения МНК представляется проблематичным (достаточно большое количество параметров и мультиколлинеарность). Ш. Алмон предложила считать, что зависимость величин коэффициентов от лагов является полиномиальной. В этом случае часть проблем, связанных с проблемами МНК снимается. Не останавливаясь подробно на теории вопроса, отметим, что если считать, что коэффициенты модели с распределёнными лагами вычисляются из соотношений В EViews модель распределённых лагов рассчитывается несколько по-иному, чем описывается в эконометрической литературе. Так, зависимость коэффициентов модели от лагов имеет вид
где с = Введено это для того, чтобы уменьшить эффект мультиколлинеарности. На конечные результаты метода это введение влияния не оказывает.  Чтобы задать в EViews расчёт модели с распределёнными лагами, необходимо в спецификации уравнения регрессии задать (y с pdl(x,l,k)). Здесь у – зависимая переменная, с – константа, х – независимая переменная, l – максимальный лаг, к – степень полинома, pdl – polynomial distributed lag (полиномиально распределённый лаг). На рисунке 5.5 приведён отчёт о работе модели pdl, заданной спецификацией (inventory с pdl(sales,3,1)), т.е. изучается зависимость запасов от продаж с лагом, равным трём годам, а степень полинома равна единице.
Рисунок 5.5 – Оценка параметров модели с распределённым лагом
Итак, в рассматриваемом примере уравнение с распределённым лагом в общем виде следующее
Коэффициенты этого уравнения рассчитываются из соотношений где На рисунке 5.5 с – это Итак, в нашем примере уравнение регрессии с распределённым лагом имеет вид Отметим, что здесь найдено не лучшее уравнение регрессии. Коэффициенты полинома, да и самого уравнения, незначимы, в остатках присутствует автокорреляция. Эти вопросы решаются отдельно и здесь не рассматриваются.
Глава 6 Единичные корни и коинтеграция
Метод Энгеля–Гренджера
Нестационарный процесс, первые разности которого стационарны, называется интегрированным первого порядка и обозначается I(1). Стационарный процесс в этих обозначениях является I(0)-рядом. Как известно, при моделировании зависимости между временными рядами на основе регрессионного анализа, важно знать, являются ли анализируемые ряды стационарными. В случае их стационарности оценки, полученные на основе МНК, будут «хорошими». Но если моделируемые временные ряды не стационарны, велика вероятность получить ложную регрессию, особенно, если эти ряды имеют детерминированные тренды. Отличить ложную регрессию от истинной можно, опираясь на теорию коинтеграции. Под коинтеграцией понимают причинно-следственную зависимость между временными рядами в течение длительного промежутка времени. В соответствии с этой теорией между временными рядами существует коинтеграция, если их линейная комбинация является стационарным временным рядом. В этом случае говорят, что временные ряды имеют между собой долгосрочную или равновесную зависимость и для её изучения можно использовать традиционный регрессионный анализ, включая t- и F-статистики. Итак, если линейная комбинация двух I(1) рядов является I(0) рядом, то эти временные ряды являются коинтегрироваными порядка 1 и обозначаются CI(1,0). Разработано несколько методов тестирования временных рядов на коинтеграцию. Рассмотрим один из них, разработанный Энгелем и Грэнджером (Engle R.F., Granger C.W.J.). Протестировать временные ряды на коинтеграцию было бы просто, если бы были известны коэффициенты их линейной комбинации. Но поскольку эта информация зачастую неизвестна, Энгель и Грэнджер предложили воспользоваться оценками этих коэффициентов, полученными из обычной регрессии с помощью МНК. Итак, пусть рассматриваются два временных ряда Другой метод тестирования коинтеграции основан на статистике Дарбина–Уотсона, рассчитанной для исходного уравнения. В этом случае проверяется гипотеза о равенстве нулю статистики Дарбина–Уотсона для генеральной совокупности. В эконометрической литературе приводится критическое значение этой статистики для разных уровней значимости (для 5%-ного уровня значимости, например, критическое значение равно 0,386). Если расчётное значение статистики Дарбина–Уотсона превышает критическое, то гипотеза об отсутствии коинтеграции отклоняется. Для примера проверим, являются ли коинтегрированными два временных ряда, изображённых на рисунке 6.1.
Рисунок 6.1 – Графики анализируемых рядов
Для этого оценим исходное уравнение регрессии У на Х (рисунок 6.2).
Рисунок 6.2 – Уравнение регрессии
На основании статистики Дарбина–Уотсона гипотезу об отсутствии коинтеграции надо отклонить. Проверим гипотезу о единичном корне для остатков этого уравнения по ADF-тесту.
Рисунок 6.3 – ADF-тест на единичный корень
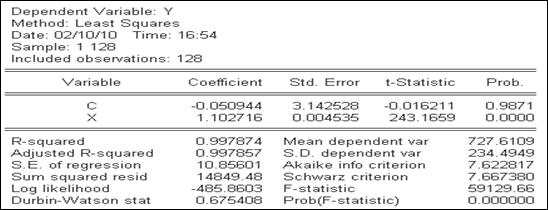
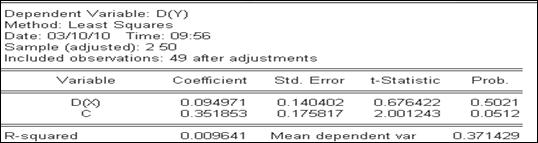
Как следует из отчёта о проверке этой гипотезы (рисунок 6.3), гипотеза о единичном корне в остатках и по этому критерию отклоняется (Prob. для t-Statistic = 0). Таким образом, остатки уравнения регрессии Чтобы подтвердить этот вывод, проверим, влияют ли изменения зависимой переменной на изменения независимой переменной. Для этого построим уравнение регрессии приращений переменной У (DY) на приращения переменной Х (DX) (рисунок 6.4).
Рисунок 6.4 – Уравнение регрессии прироста У на прирост Х
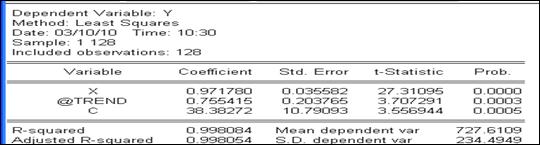
Как видим, изменения Х объясняют изменения У (Prob. для D(X ) < 0,05). Кроме того, при включении в исходное уравнение регрессии фактора времени (рисунок 6.5), независимая переменная по-прежнему оказалась значимой. Это лишний раз подтверждает тот факт, что изменение независимой переменной объясняет изменение зависимой переменной, т.е. между этими переменными действительно наблюдается причинно-следственная связь.
Рисунок 6.5 – Уравнение регрессии с фактором времени Ложная регрессия
Приведём теперь пример ложной регрессии. Пусть рассматриваются следующие два временных ряда (рисунок 6.6). Как видим, оба ряда имеют явный тренд. Составим уравнение регрессии (рисунок 6.7) и протестируем его остатки на единичный корень (рисунок 6.8).
Рисунок 6.6 – Пример ложной регрессии
Рисунок 6.7 – Уравнение регрессии для случая ложной регрессии
Как видим, точность уравнения довольно высокая (R-squared = 0,92) и остатки не автокоррелированы (DW = 2,16) и тест на единичный корень (рисунок 6.8) подтверждает, что временной ряд остатков является стационарным рядом. Однако уравнение регрессии приращения У на приращения Х (рисунок 6.9) показывает, что изменение Х не объясняет изменение У (Prob для D(X) > 0,05). Кроме того, включение в уравнение регрессии фактора времени (рисунок 6.10) показывает, что фактор времени значимо влияет на изменение зависимой переменной, а переменная Х оказалась незначимой. Таким образом, в данном случае изменение переменной У зависит только от изменения времени, но не от изменения переменной Х. Последнее утверждение подтверждается и уравнением линейного тренда для зависимой переменной (рисунок 6.11). Эта зависимость более тесная, чем в случае зависимости У от Х.
Рисунок 6.8 – Тест на единичный корень
Рисунок 6.9 – Уравнение регрессии D(Y) на D(X)
Рисунок 6.10 – Уравнение регрессии с фактором времени
Рисунок 6.11 – Уравнение тренда для переменной У
Таким образом, в этом примере (рисунок 6.7) имеем ложную регрессию, которая отражает лишь тот факт, что обе переменные имеют линейные тренды. Глава 7 Векторная авторегрессия
Общие положения
Векторная авторегрессия – это такая модель, в которой изучаются несколько зависимых переменных, зависящих от собственных лагов и от лагов других переменных. Наибольший порядок запаздываний, включаемых в правую часть, называется порядком векторной авторегрессии. Если этот порядок равен р, то для такой модели используют обозначение VAR(p). Модели векторной авторегрессии (Vector Autoregression – VAR) можно рассматривать как некий гибрид моделей одномерных временных рядов и систем одновременных уравнений. При их применении не приходится решать вопросы отнесения той или иной переменной к эндогенным или экзогенным переменным, что не совсем просто. Кроме того, эти модели позволяют исследовать зависимости с более сложной структурой, чем в анализе одномерных временных рядов или с использованием более сложных систем одновременных систем уравнений, что во многих случаях обеспечивает более высокое качество прогнозов. К недостаткам VAR-моделей можно отнести неопределённость в выборе подходящей длины лага, значительное число оцениваемых параметров и то, что все переменные в модели должны быть стационарными. Данные проблемы решаются дополнительными исследованиями (имитационное моделирование, преобразование переменных и т.п.). Рассмотрим частный случай, когда рассматриваются две переменные и зависят они от лаговых значений этих переменных до второго порядка включительно. Такая модель(VAR(2)) имеет вид
где Запишем эту модель в матричном виде, введя обозначения
Получим Известно, что условием стабильности такой модели является тот факт, что все обратные корни уравнения det Приведём пример оцененной VAR, используя временные ряды на рисунке 6.1. Закажем VAR(2), выбрав «Proc/Make Vector Autoregression…». Получим диалоговое окно спецификации VAR-модели (рисунок 7.1).
Рисунок 7.1 – Окно спецификации VAR-модели
По умолчанию устанавливается VAR(2) с константой в качестве экзогенных переменных. Щёлкнув «ОК», получим оценку VAR-модели (рисунок 7.2). Для каждого уравнения VAR-модели здесь рассчитываются традиционные показатели их точности. Как указано в заголовке окна отчёта, под оценками параметров в круглых скобках показаны стандартные ошибки оценок, а ниже (в квадратных скобках) – соответствующие t-статистики. Считается, что если t–статистика меньше двух, то оценка незначимо отлична от нуля. Если ориентироваться на это, то значимо отличаются от нуля в первом уравнении – только оценка при переменной
Рисунок 7.2 – Оценка VAR-модели
Оцененная VAR-модель имеет вид (с округлением во втором знаке и без учёта значимости оценок)
Ниже (рисунок 7.3) приведена проверка VAR-модели на стабильность. Как видим, условие стабильности не выполняется (один из корней больше единицы).
Рисунок 7.3 – Проверка VAR-модели на стабильность |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
 (полиномы от лага степени к), то исходное уравнение можно заменить на уравнение от вспомогательных переменных с коэффициентами
(полиномы от лага степени к), то исходное уравнение можно заменить на уравнение от вспомогательных переменных с коэффициентами 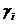 . Вспомогательные переменные являются линейными комбинациями исходной независимой переменной и её лаговых значений. Их число равно к, а поскольку это число, как правило, меньше максимального лага, то размерность вспомогательного уравнения будет меньше размерности исходного уравнения. Оценив вспомогательное уравнение, определим
. Вспомогательные переменные являются линейными комбинациями исходной независимой переменной и её лаговых значений. Их число равно к, а поскольку это число, как правило, меньше максимального лага, то размерность вспомогательного уравнения будет меньше размерности исходного уравнения. Оценив вспомогательное уравнение, определим  , (j = 0,1,2,…,l),
, (j = 0,1,2,…,l), .
.
 .
.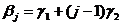 (здесь c=k/2=1). Вспомогательное уравнение имеет вид
(здесь c=k/2=1). Вспомогательное уравнение имеет вид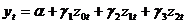 ,
, – линейные комбинации текущих и лаговых значений независимой переменной.
– линейные комбинации текущих и лаговых значений независимой переменной. , PDLoj – это
, PDLoj – это  (j=1,2,3), а коэффициенты
(j=1,2,3), а коэффициенты  (j=0,1,2) – это числа в последней части отчёта. Левее их помещён график распределения лагов.
(j=0,1,2) – это числа в последней части отчёта. Левее их помещён график распределения лагов.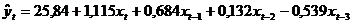 .
. и
и  . Для них составляется уравнение регрессии вида
. Для них составляется уравнение регрессии вида  , параметры которого оцениваются обычным МНК. Чтобы проверить коинтегрированы ли эти ряды, предлагается протестировать остатки коинтеграционного уравнения на стационарность с помощью, например, теста Дики–Фуллера. Пусть
, параметры которого оцениваются обычным МНК. Чтобы проверить коинтегрированы ли эти ряды, предлагается протестировать остатки коинтеграционного уравнения на стационарность с помощью, например, теста Дики–Фуллера. Пусть  – остатки этого уравнения. Проверка нулевой гипотезы об отсутствии коинтеграции в методе Энгеля–Гренджера проводится с помощью регрессии
– остатки этого уравнения. Проверка нулевой гипотезы об отсутствии коинтеграции в методе Энгеля–Гренджера проводится с помощью регрессии 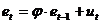 . Причём, проверяется гипотеза о равенстве единице коэффициента при переменной
. Причём, проверяется гипотеза о равенстве единице коэффициента при переменной  с помощью t-статистики. Проще такую проверку проводить, преобразовав это уравнение к виду
с помощью t-статистики. Проще такую проверку проводить, преобразовав это уравнение к виду  , где
, где  . В данном случае проверяется гипотеза
. В данном случае проверяется гипотеза  :
:  против альтернативной гипотезы
против альтернативной гипотезы  . Как и в тесте Дики-Фуллера, t-статистика при проверке этой гипотезы имеет распределение, отличное от распределения Стьюдента, и для неё рассчитаны свои критические значения.
. Как и в тесте Дики-Фуллера, t-статистика при проверке этой гипотезы имеет распределение, отличное от распределения Стьюдента, и для неё рассчитаны свои критические значения.

 (рисунок 6.2) стационарны, следовательно, эти два временных ряда коинтегрированы, а само уравнение является уравнением долгосрочного равновесного соотношения и отражает истинную зависимость между этими временными рядами.
(рисунок 6.2) стационарны, следовательно, эти два временных ряда коинтегрированы, а само уравнение является уравнением долгосрочного равновесного соотношения и отражает истинную зависимость между этими временными рядами.







 и
и  – независимые случайные величины, следующие N(0,
– независимые случайные величины, следующие N(0,  ). Называются они по-разному: инновации, шоки, импульсы. Оценивают параметры таких моделей обычным МНК, применяемым к каждому уравнению отдельно.
). Называются они по-разному: инновации, шоки, импульсы. Оценивают параметры таких моделей обычным МНК, применяемым к каждому уравнению отдельно.






 или
или  . Последнее выражение можно представить как
. Последнее выражение можно представить как  где L – лаговый оператор.
где L – лаговый оператор. лежат за пределами единичного круга, т.е. модули этих корней больше единицы. В отчёте о стабильности в EViews отражаются величины, обратные к этим корням, поэтому условием стабильности будем считать наличие всех корней, по модулю меньших единице.
лежат за пределами единичного круга, т.е. модули этих корней больше единицы. В отчёте о стабильности в EViews отражаются величины, обратные к этим корням, поэтому условием стабильности будем считать наличие всех корней, по модулю меньших единице.
 , а во втором уравнении – при переменных
, а во втором уравнении – при переменных  и
и  .
.