Процесс случайного блуждания и единичный корень

При анализе временных рядов важно знать является ли ряд стационарным. Рассмотрим стационарный AR(1) процесс или процесс Маркова:  с , N(0, ). Используя лаговый оператор, перепишем это выражение в виде  или . Откуда имеем, что корень лагового оператора  равен (1/ ), который при условии  больше единицы. Таким образом, нестационарный процесс случайного блуждания имеет единичный корень, а стационарный AR(1) процесс – корень, меньший единице. Поэтому, чтобы протестировать временной ряд АR(1) на стационарность, достаточно рассмотреть нулевую гипотезу  против альтернативной гипотезы .

Итак, одним из методов тестирования временного ряда на стационарность является проверка гипотезы о единичном корне в уравнении . Как известно, осуществить эту проверку можно на основании t-статистики . Однако, как показали Дики и Фуллер (D.A.Dickey, W.A.Fuller), если верна нулевая гипотеза о единичном корне, то эта статистика не следует распределению Стьюдента. Фуллер построил таблицу для определения критических значений этой статистики методом Монте–Карло, отсюда и название теста (Dickey–Fuller unit-root tests).

Чтобы было удобнее тестировать гипотезу о единичном корне, исходное уравнение  преобразовывается к виду  или, после замены , к виду . Тогда нулевая гипотеза формулируется в виде , альтернативная гипотеза имеет вид . Тестируется  на основе t-статистики , которая, если верна , имеет DF-t-распределение. Критические значения этой статистики зависят от вида тестируемой модели, а именно – включены ли в модель константа или константа и детерминированный тренд. Соответствующий запрос появится в диалоговом окне, при вызове процедуры теста Дики–Фуллера (рисунок 4.3).

Рисунок 4.3 – Диалоговое окно теста на единичный корень

Как видим, в позиции «Include in test equation – включить в тестовое уравнение» предполагается три варианта: включить в тестовое уравнение пересечение (константу), тренд и пересечение и ни того, ни другого. На рисунке 4.3 выбрана процедура включения в модель константы (Intercept). В позиции «Test for unit root in – тест на единичный корень в» предлагается также три варианта модели: в уровнях временного ряда, в первых разностях и во вторых разностях (на рисунке 4.3 выбрано в уровнях «Level»). Кроме того, в позиции «Automatic selection – выбор автоматически» проставлен информационный критерий Шварца и указано максимальное число лагов – 9. По указанному критерию в автоматическом режиме выбирается оптимальное число лаговых значений анализируемого ряда.

Дело в том, что DF-тест используется только для AR(1)-процессов, т.е. остатки в тестируемой модели не должны быть автокоррелированными (в противном случае тест не эффективен). В общем случае в рассматриваемый тест включаются слагаемые остатков более высокого порядка автокорреляции, при этом оптимальный лаг по умолчанию подбирается на основе информационного критерия Шварца (возможно также использование и других критериев). Известно, что включение в тестовое уравнение лаговых значений остатков не влияет на критические значения ADF-t-статистики. Такой тест называется расширенным тестом Дики–Фуллера (Augmented Dickey-Fuller test) (см. рисунок 4.3 в позиции «Test type»).

Рисунок 4.4 – Тестируемый временной ряд

Для иллюстрации работы теста приведём результаты тестирования ряда, график которого показан на рисунке 4.4. Поскольку в предлагаемом для тестирования ряду наблюдается слабый тренд, включим в тестирование первые разности и константу (рисунок 4.5). Известно, что если данные временного ряда следуют линейному тренду, то их первые разности являются стационарным временным рядом.

Итак, проверяется гипотеза о том, что первые разности уровней анализируемого временного ряда имеют единичный корень. Расчётное значение ADF-t-статистики (Augmented Dickey-Fuller Test statistic) равно     (-4,72898). Здесь тест односторонний, поэтому нулевая гипотеза отклоняется (Prob. < 0,05). Далее в отчёте приведены критические значения t-статистики (Test critical values) для разных уровней значимости. Все они правее вычисленного значения, т.е. расчётное значение t-статистики попало в критическую область.

Рисунок 4.5 – Результаты теста Дики–Фуллера

Как видим в нижней части рисунка 4.5, в модель для тестирования гипотезы о единичном корне были включены: слагаемые, учитывающие автокорреляцию первого порядка (D(Y(-1))) и константа (С). Тест показал, что первые разности уровней анализируемого временного ряда стационарны.

Следует отметить, что первоначальная версия теста предполагала, что тестированию на единичный корень подвергаются «сырые» временные ряды. Однако если тестированию подвергаются временные ряды остатков, которые получаются после предварительного оценивания какой-либо модели, то ситуация меняется. В этом случае  МНК выбирает остатки так, что даже если они не стационарны, то становятся похожими на стационарные. Поэтому распределение соответствующих статистик в этом случае другое, и пользоваться ранее рассмотренными критическими величинами не рекомендуется (в этом случае гипотеза о единичном корне отклоняется слишком часто). С учётом этого были рассчитаны другие критические значения ADF-t-статистики, позволяющие анализировать, в том числе и остатки моделей.

Если протестировать на единичный корень временной ряд, показанный на рисунке 4.1, то вывод о его стационарности, сделанный на основе анализа коррелограммы, (рисунок 4.2) подтверждается и этим тестом (рисунок 4.6).

Рисунок 4.6 – Тест на единичный корень

Модели Бокса–Дженкинса

При моделировании стационарных временных рядов часто используют модели авторегрессии (AR(p)) и скользящего среднего (MA(q)), где p и q – порядок модели.

Модель авторегрессии порядка рAR(p) может быть записана:

,

а модель скользящего среднего порядка q MA(q) имеет следующий вид:

.

Смешанная модель авторегрессии и скользящего среднего ARMA(p,q) объединяет обе эти модели в одну:

.

Если ряд не стационарный, но его можно привести к стационарному виду путём взятия разностей, то используется модель ARIMA(p,d,q), где d – порядок разности. В этом случае модель ARMA(p,q) строится не для уровней элементов временного ряда, а для их разностей.

Не останавливаясь подробно на теории методологии Бокса–Дженкинса, отметим лишь, что при использовании этих методов приходится решать вопросы выбора порядка модели (её спецификации) и тестирования её на адекватность.

В эконометрической литературе отмечается, что обычно порядок модели выбирается из условия, что p+q не должно превышать трёх, а d – не более двух. Поэтому не представляет больших затруднений при выборе типа модели просто перебрать значения этих параметров в указанных пределах и протестировать эти модели на точность и адекватность. Точность моделей обычно оценивается на основе традиционных показателей (коэффициент детерминации, стандартная ошибка и т.п.), а адекватность – на основе анализа поведения остатков (например, исследовать коррелограмму остатков с использованием Q-статистики). Остатки не должны содержать информации, на основе которой можно уточнить прогноз по модели. При этом рекомендуется придерживаться принципом экономии, а именно: при примерно одинаковых по точности моделях предпочтение отдаётся более простой модели. При этом рекомендуется пользоваться информационными критериями Акаике и Шварца.

Для определения спецификации модели информацию можно получить на основе обычных t-статистик при коэффициентах модели. Незначимые коэффициенты покажут, какие слагаемые из модели можно удалить.

Проиллюстрируем работу этих моделей на примере следующего временного ряда (рисунок 4.7).

Рисунок 4.7 – График анализируемого ряда

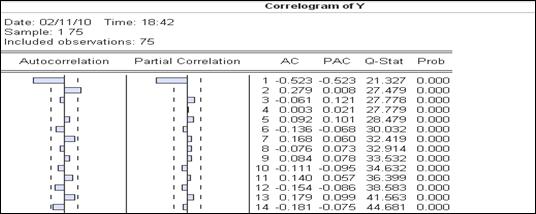
По графику (рисунок 4.7) видно, что ряд вроде бы стационарный, но коррелограмма показывает (рисунок 4.8), что в уровнях ряда есть тренд (первые два коэффициента автокорреляции отличны от нуля).

Рисунок 4.8 – Коррелограмма уровней временного ряда

ADF-тест на единичный корень первых разностей (рисунок 4.9) показывает, что ряд первых разностей стационарный.

Рисунок 4.9 – ADF-тест на единичный корень первых разностей

Применим к рассматриваемому ряду метод Бокса–Дженкинса, перебирая различные варианты моделей авторегрессии-скользящего среднего для первых разностей. Начнём с модели ARIMA(1,1,2).

Спецификация ARIMA(1,1,2)-модели в EViews задаётся командой (на рисунок 4.10 выделено).

Рисунок 4.10 – Спецификация ARIMA(1,1,2)-модели

Здесь d(y) означает, что рассматриваются первые разности ряда y, затем указаны члены модели: константа, авторегрессия первого порядка (ar(1))  и скользящие средние первого и второго порядков (ma(1) и ma(2)). Результаты оценивания параметров этой модели приведены на рисунке 4.11.

Рисунок 4.11 – Оценка параметров модели ARIMA(1,1,2)

Удалив из модели незначимые константу и член ma(2), получим   (рисунок 4.12)

Рисунок 4.12 – Оценка параметров модели ARIMA(1,1,1)

Обе модели практически одинаковы по точности, но на основании принципа экономии выбираем вторую модель (рисунок 4.12). Тем более что по информационному критерию Шварца эта модель предпочтительней. Графическое представление этой модели выглядит так (рисунок 4.13).

Рисунок 4.13 – Графическое представление расчётов по модели ARIMA(1,1,1)

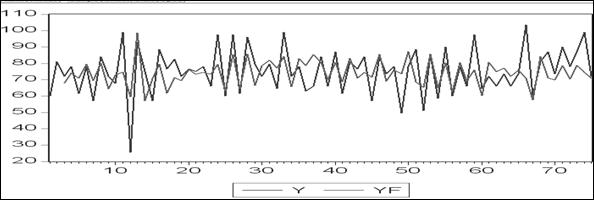
Сделаем прогноз по этой модели (динамический и статический варианты). Хотя модель составлена для разностей, прогноз закажем для уровней временного ряда. На рисунке 4.14 приведены два ряда: исходный (Y) и предсказанный по статическому прогнозу (YF), а на рисунке 4.13 (верхняя часть) – исходный ряд (Actual) и ряд, рассчитанный на основе оценённой модели (Fitted).

Рисунок 4.14 – Прогноз по модели ARIMA(1,1,1)

Ряды YF и Fitted – это разные ряды. Это видно и по графикам (рисунок 4.13 и  рисунок 4.14). Ряд Fitted рассчитывался по модели , а ряд YF – по другой модели . Во втором случае в модель подставляется не фактическое значение разности лаговой переменной , а расчётное – , полученное из первой модели.

Рисунок 4.15 – Тест на единичный корень

Тест на единичный корень в остатках модели (рисунок 4.15) показывает, что модель адекватна исходным данным.

Остановимся на различных видах прогнозов, реализованных в EViews. Как известно, различают динамический и статический прогнозы. При динамическом методе прогнозирования в модель, имеющей в качестве независимых переменных лаговые значения зависимой переменной, каждый раз подставляются расчётные значения лаговых переменных, а в варианте статического прогнозирования – фактические значения. А потому эти два вида прогнозов дают разные результаты (рисунки 4.16 и 4.17).

Рисунок 4.16 – Динамический прогноз, начиная с 60-го наблюдения

Рисунок 4.17 – Статический прогноз, начиная с 60-го наблюдения

При динамическом прогнозе прогнозные значения постепенно стабилизируются, а при статическом – в большей мере следуют за фактическими значениями. Статический и динамический прогнозы различаются, если в модели справа присутствуют лаговые значения зависимой переменной.