Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение регрессии с гетероскедастичными остатками(взвешенный метод наименьших квадратов)
Итак, важно уметь тестировать уравнение регрессии на гетероскедастичность и в случае её обнаружения уметь смягчить проблемы, связанные с ней. Одним из методов решения этой проблемы является использование взвешенного МНК (ВМНК). Обычный МНК минимизирует сумму квадратов отклонений Проиллюстрируем работу ВМНК на следующем примере. Пусть имеется следующая информация по регионам: y – расходы на образование, x1 – валовой региональный продукт, x2 – численность населения. Оценим уравнение регрессии зависимости расходов на образование от перечисленных переменных (рисунок 3.29). 
Рисунок 3.29 – Исходное уравнение регрессии
Как видно (рисунок 3.30), остатки этого уравнения гетероскедастичны, что подтверждает и тест White (рисунок 3.31) – Probability для Obs*R-squered < 0,05.
Рисунок 3.30 – График остатков исходного уравнения
Рисунок 3.31 – Тест White для исходного уравнения
Визуальный анализ графика остатков (рисунок 3.30) даёт основание предположить, что дисперсия отклонений зависимой переменной пропорциональна величине зависимой переменной. А как показывает корреляционная матрица (рисунок 3.32), все три переменные взаимозависимы, следовательно, можно предположить, что остатки пропорциональны зависимым переменным.
Рисунок 3.32 – Матрица парных коэффициентов корреляции
Это даёт основание (для преодоления гетероскедастичности) взять в качестве весов значения одной из независимых переменных. Разделим все переменные в спецификации исходного уравнения на корень квадратный из x2. В этом случае вместо уравнения
Рисунок 3.33 – Спецификация уравнения для реализации ВМНК
Оценив это уравнение, получим (рисунок 3.34).
Рисунок 3.34 – Оценка уравнения по ВМНК
График остатков этого уравнения представлен на рисунок 3.35. Как видим, чётко выраженной гетероскедастичности здесь не наблюдается, о чём свидетельствует и тест Уайта (рисунок 3.36) (Probability для Obs*R-squered = 0,3326, что > 0,05).
Рисунок 3.35 – График остатков преобразованного уравнения
Рисунок 3.36 – Тест White для преобразованного уравнения
Сравнивая оценки параметров последних двух уравнений (исходного (рисунок 3.29) и преобразованного (рисунок 3.34)), видим, что коэффициент при переменной А теперь проиллюстрируем работу взвешенного МНК, реализованного в EViews. Для этого рассмотрим эту же самую информацию и в качестве весов для ВМНК возьмём те же веса (1/х2^0,5). Реализация этой процедуры следующая. После оценки исходного уравнения (рисунок 3.34), выбираем «Proc/Specify/Estimate…» и в заставке «Option» окна «Equation Estimation» вывешиваем флажок для «Weighted LS\TSLS», а в окно «Weight» заносим «1/х2^0,5» (рисунок 3.37).
Рисунок 3.37 – Диалоговое окно для организации взвешенного МНК
Тем самым мы заказали взвешенный МНК с весами (1/х2^0,5). Щёлкнув «ОК», получим реализацию этого метода (рисунок 3.38).
Рисунок 3.38 – Реализация ВМНК
Сравнивая с рисунком 3.34, видим, что получили то же самое уравнение (в смысле оценённых коэффициентов уравнения регрессии), но более «экономным» путём. В нижней части отчёта (рисунок 3.38) для сравнения представлена информация о точности исходного уравнения (Unweighted Statistics). Приведённый пример только иллюстрирует механизм реализации ВМНК. Не всегда удаётся просто решить проблему гетероскедастичности. Это достаточно трудоёмкая задача. На практике имеет смысл применить несколько методов определения гетероскедастичности и способов её корректировки, приводящих к стабилизации дисперсии остатков.
Мультиколлинеарность
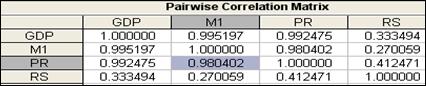
Переменные считаются коллинеарными, если коэффициент корреляции между ними больше 0,7-0,8. Если таких переменных несколько, то говорят, что имеет место мультиколлинеарность. Мультиколлинеарность представляет серьёзную проблему для регрессионного анализа. В этом случае определитель матрицы (XTX) из формулы (3.4) близок к нулю, поэтому элементы обратной матрицы (XTX)-1 принимают большие значения (при вычислении обратной матрицы элементы союзной матрицы делятся на определитель исходной матрицы, а он близок к нулю) и стандартные ошибки коэффициентов регрессии Проиллюстрируем сказанное на ранее рассмотренном примере (рисунок 3.4). Рассчитаем матрицу парных коэффициентов корреляции для анализируемых переменных (рисунок 3.39).
Рисунок 3.39 – Матрица парных коэффициентов корреляции
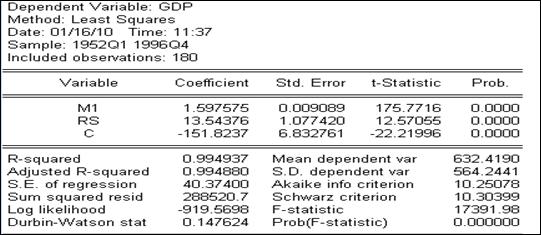
Видим, что переменные M1 и PR коллинеарные. Посмотрим, как это отразилось на оценках параметров. Оценив уравнение регрессии с полным набором переменных (рисунок 3.4), мы видели, что переменная RS оказалась незначимой. В условиях коллинеарности это ничего не означает, т.к. не значимость может оказаться результатом того, что оценки параметров сосчитаны с большими ошибками как раз за счёт коллинеарности. В самом деле, рассчитав уравнение регрессии с другой исключённой переменной, которая в полном уравнении была значимой (PR), получим, что теперь переменная RS оказалась значимой (рисунок 3.40), и оценка коэффициента при ней существенно изменилась (по сравнению со случаем полной регрессии (была 0,46, стала 13,5)). Изменилась так же и оценка коэффициента при M1 (была 0,95, стала 1,6). Точность уравнения регрессии при этом значимо не изменилась.
Рисунок 3.40 – Уравнение регрессии без переменной PR
Исключим теперь из полного уравнения переменную М1 (рисунок 3.41). Получили, что точность уравнения регрессии снова изменилась не значимо, а коэффициенты уравнения регрессии изменились существенно (при переменной RS даже изменился знак). Определить, какой же на самом деле должен быть коэффициент при каждой переменной в случае мультиколлинеарности не представляется возможным, т.к. каждый из них должен показывать, на сколько изменится зависимая переменная при изменении независимой переменной на единицу при фиксированных значениях других переменных. В случае же коллинеарности нельзя изменить одну переменную при неизменности других, т.к. они тесно взаимосвязаны.
Рисунок 3.41 – Уравнение регрессии без переменной М1
Проблема мультиколлинеарности не всегда существенна. Если уравнение регрессии оценивается с целью использовать его для прогнозирования и оно точное, то мультиколлинеарность не представляет затруднений при решении этой задачи. Но если уравнение регрессии предполагается использовать для анализа влияния независимых переменных на зависимую, то мультиколлинеарность здесь будет представлять существенную проблему. Однозначного решения проблемы мультиколлинеарности не существует, поскольку причины мультиколлинеарности могут быть разными. В нашем примере речь идёт о временных рядах, поэтому можно попробовать построить уравнение регрессии не на уровни рядов, а на их первые разности. Действительно, построив матрицу парных коэффициентов корреляции по первым разностям (рисунок 3.42), видим, что новые независимые переменные не коллинеарны.
Рисунок 3.42 – Матрица парных коэффициентов корреляции для разностей
При построении этой матрицы необходимо предварительно сгенерировать первые разности анализируемых переменных. Для этого в строке команд надо записать: genr dgdp = d(gdp) (верхняя часть рисунка 3.42). Тем самым под именем DGDP будет создана переменная, представляющая собой первые разности переменной GDP. Аналогично и для других переменных. Оценив уравнение регрессии для первых разностей, получим (рисунок 3.43).
Рисунок 3.43 – Уравнение регрессии для первых разностей
Как видим, все переменные оказались значимыми (в отличие от случая с исходными данными (рисунок 3.4)). После построения уравнения регрессии по разностям не сложно перейти к уровням исходных переменных. Если моделируемые временные ряды имеют детерминированные тренды, то от мультиколлинеарности помогает избавиться введение в регрессию фактора времени, как трендовой составляющей. Чтобы ввести переменную времени, её надо сначала сгенерировать. Для этого в окне команд надо набрать genr t = @trend, а потом эту переменную (t) вставить в список регрессоров. Получим (рисунок 3.44).
Рисунок 3.44 – Уравнение регрессии с фактором времени Как видим, переменная RS стала значимой и оценка параметра при ней существенно изменилась по сравнению с уравнением без фактора времени (рисунок 3.4). Оценки параметров при остальных переменных существенно не изменились. Кроме рассмотренного приёма, для преодоления проблемы мультиколлинеарности рекомендуется избавиться от одного или нескольких тесно связанных регрессоров, получить дополнительные данные или изменить спецификацию модели, преобразовать переменные, использовать гребневую регрессию и т.д.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 423. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , в которую все слагаемые входят с одними и теми же весами (равными единице). В этом случае большие отклонения (не точные наблюдения) дают больший вклад в результат анализа а, по идее, должно быть наоборот. Чтобы компенсировать этот недостаток МНК в случае гетероскедастичных остатков, предлагается взвешивать квадраты отклонений, приписывая большим отклонениям меньшие веса и наоборот. Основная проблема здесь – как определить эти веса. Одним из методов её решения – выяснить есть ли зависимость между величиной отклонений и какой-либо независимой переменной, и взять обратные значения этой переменной в качестве весов. Если такая зависимость линейная (
, в которую все слагаемые входят с одними и теми же весами (равными единице). В этом случае большие отклонения (не точные наблюдения) дают больший вклад в результат анализа а, по идее, должно быть наоборот. Чтобы компенсировать этот недостаток МНК в случае гетероскедастичных остатков, предлагается взвешивать квадраты отклонений, приписывая большим отклонениям меньшие веса и наоборот. Основная проблема здесь – как определить эти веса. Одним из методов её решения – выяснить есть ли зависимость между величиной отклонений и какой-либо независимой переменной, и взять обратные значения этой переменной в качестве весов. Если такая зависимость линейная (  ), то делением на
), то делением на  обеих частей уравнения можно добиться выполнение условия гомоскедастичности. В этом случае преобразованный остаточный член (
обеих частей уравнения можно добиться выполнение условия гомоскедастичности. В этом случае преобразованный остаточный член (  ) будет удовлетворять условию гомоскедастичности. В случае если такую переменную найти не удаётся, предлагается вместо неё использовать линейную комбинацию всех переменных, по сути дела, в качестве весов взять оценённые значения зависимой переменной (
) будет удовлетворять условию гомоскедастичности. В случае если такую переменную найти не удаётся, предлагается вместо неё использовать линейную комбинацию всех переменных, по сути дела, в качестве весов взять оценённые значения зависимой переменной (  ).
).



 будет оценена зависимость вида
будет оценена зависимость вида  (рис. 3.33).
(рис. 3.33).



 изменился значимо (был (-0,053), стал (-0,083)). Остальные два изменились незначимо (константа равна нулю в обоих уравнениях).
изменился значимо (был (-0,053), стал (-0,083)). Остальные два изменились незначимо (константа равна нулю в обоих уравнениях).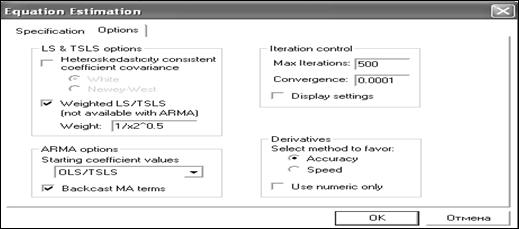

 (3.5) существенно увеличиваются. В этом случае оценки параметров уравнения регрессии принимают неоправданно большие значения, рассчитываются с большими ошибками, становятся неустойчивыми и теряют свою познавательную ценность.
(3.5) существенно увеличиваются. В этом случае оценки параметров уравнения регрессии принимают неоправданно большие значения, рассчитываются с большими ошибками, становятся неустойчивыми и теряют свою познавательную ценность.