Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Проверка остаточного члена на автокорреляцию
А теперь обсудим статистику Дарбина–Уотсона. Эта статистика проверяет выполнимость предпосылки об отсутствии автокорреляции в остаточном члене уравнения регрессии, но в укороченном её варианте, а именно: отсутствие автокорреляции первого порядка. Рассчитывается эта статистика из соотношения DW = Легко показать, что DW Для DW-статистики найдены критические границы (du – верхняя и dl – нижняя), на основе которых можно определить области, позволяющие принять или отклонить нулевую гипотезу об отсутствии автокорреляции при фиксированном уровне значимости (
0 dl du 4-du 4-dl 4 Рисунок 3.6 – Механизм проверки остатков на автокорреляцию
Если вычисленное значение DW-статистики попало в область неопределённости критерия, то это означает, что нет статистических оснований ни принять, ни отклонить нулевую гипотезу об отсутствии автокорреляции в остатках. В этом случае нужно использовать какой-либо иной критерий или для большей точности увеличить объём выборки. Учитывая наличие области неопределённости, в литературе по эконометрике можно встретить такую рекомендацию: считать, что автокорреляции в остатках нет, если значение критерия находится в интервале (1,5–2,5), в противном случае признаётся наличие автокорреляции.  Рассмотрим «сокращённое» уравнение (рисунок 3.5). Для него DW = 0,13. По всем признакам в этом уравнении автокорреляция в остатках присутствует, т.е. обсуждаемая предпосылка МНК нарушена. Посмотрим на поведение остатков в нашем уравнении. Для этого в окне отчёта об уравнении регрессии выберем «View/Actual,Fitted,Residual/Actual,Fitted,Residual Graph» (рисунок 3.7) и получим (рисунок 3.8).
Рисунок 3.7 – Выбор процедуры просмотра графика остатков
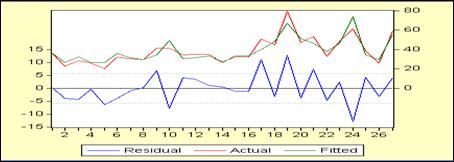
Рисунок 3.8 – Графики остатков, фактических и расчётных значений зависимой переменной
Как видим, случайности в поведении остатков не наблюдается. Они регулярно то положительные, то отрицательные. Это и есть их автокорреляционная зависимость, что и показала DW-статистика. У DW-статистики есть ограничения по её использованию:
В пакете EViews реализован ещё один тест на автокорреляцию в остатках, лишённый указанных недостатков. Этот тест разработан двумя авторами и носит их имя – тест Бреуша–Годфри (Breusch and Godfrey). Идея этого теста в следующем. Сначала обычным МНК оценивается исходное уравнение регрессии. Затем составляется вспомогательное уравнение регрессии зависимости остатков исходного уравнения от константы, исходных независимых переменных и от лаговых значений остатков исходного уравнения. Число лаговых значений остатков во вспомогательном уравнении определяется эмпирически. Затем оценивается вспомогательное уравнение и рассчитывается статистика Опишем этот тест формально. Пусть рассматривается следующее уравнение.
Чтобы протестировать остаточный член уравнения на автокорреляцию, оценим это уравнение и составим вспомогательное уравнение
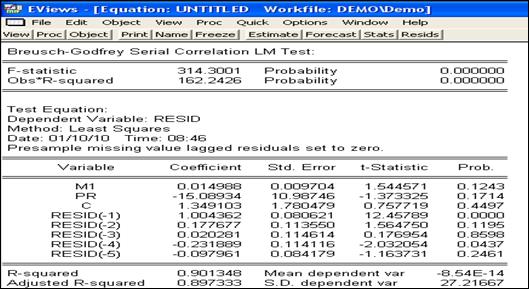
Проверяется нулевая гипотеза В этом отчёте оценено вспомогательное уравнение. Зависимая переменная (RESID) – это остатки исходного уравнения. В списке независимых переменных перечислены исходные переменные (см. рисунок 3.5) и пять лаговых значений остатков исходного уравнения. R-squared = 0.901348, а Obs*R-squared, т.е.
Рисунок 3.9 – Тест Бреуша-Годфри
Некоторые соображения по поводу анализа автокорреляции в остатках. Все вышеприведённые рассуждения, скорее относятся к случаю, когда строится уравнение регрессии на временные ряды. Если же рассматривается пространственная информация, то не совсем понятно, что же означает автокорреляция в остатках. Ведь в этом случае рассматривается случайная выборка и наблюдения следуют друг за другом в случайном порядке. Что же тогда означает последовательная автокорреляция? Проще, когда речь идёт о простой или парной регрессии. Тогда, упорядочив информацию относительно значений независимой переменной, можно говорить о последовательной автокорреляции. Появляется смысл этого термина, а именно – последовательная, т.е. по мере увеличения значений независимой переменной, а не случайная последовательность. В этом случае появляется смысл в наличии автокорреляции в остатках. Например, это может означать, что был выбран неправильный вид зависимости. Хотя и здесь не всё просто. Рассмотрим два примера. Пусть сначала имеем следующее уравнение регрессии (рисунок 3.10), где переменные означают валовой региональный продукт (GRP) и уровень заработной платы (PAY) по 27 регионам. Для случайной выборки гипотеза об отсутствии автокорреляции в остатках отклоняется (рисунок 3.11).
Рисунок 3.10 – Уравнение регрессии для случайной выборки
Рисунок 3.11 – Тест Бреуша–Годфри
А теперь эта же самая информация, упорядоченная по возрастанию независимой переменной, даёт следующее уравнение регрессии (рисунок 3.12).
Рисунок 3.12 – Уравнение регрессии для упорядоченной выборки
Рисунок 3.13 – Тест Бреуша–Годфри
Обратите внимание, изменилась только статистика Дарбина–Уотсона. Тест Бреуша-Годфри показывает, что автокорреляция в остатках отсутствует (рисунок 3.13). Означает ли это, что уравнение регрессии для случайной выборки не корректно, а для упорядоченной выборки – корректно? Уравнения-то одинаковые. Да и анализ графиков остатков мало что проясняет (рисунок 3.14 и рисунок 3.15).
Рисунок 3.14 – График остатков регрессии для случайной выборки
Рисунок 3.15 – График остатков регрессии для упорядоченной выборки
А вот другой пример. Рассматривается следующее уравнение регрессии (рисунок 3.16). Здесь y – потребление, x – доходы. Зависимость (обратная для х) явно выбрана не корректно. Но статистика DW для случайной выборки это «не заметила» (DW = 2,17).
Рисунок 3.16 – Уравнение регрессии для случайной выборки
Рисунок 2.17 – Тест Бреуша–Годфри для случайной выборки
Да и тест Бреуша–Годфри (рисунок 3.17) указывает, что автокорреляции в остатках нет. Рассчитаем теперь уравнение регрессии для упорядоченной выборки (рисунок 3.18).
Рисунок 3.18 – Уравнение регрессии для упорядоченной выборки
Статистика Дарбина–Уотсона уменьшилась, а тест Бреуша–Годфри (рисунок 3.19) указывает на наличие автокорреляции в остатках.
Рисунок 3.19 – Тест Бреуша–Годфри для упорядоченной выборки
Посмотрим теперь на графики остатков этих уравнений. На рисунке 3.20 график для случайной выборки, а на рисунке 3.21 – для упорядоченной.
Рисунок 3.20 – График остатков регрессии для случайной выборки
Рисунок 3.21 – График остатков регрессии для упорядоченной выборки
Как видим, неверная спецификация выяснилась лишь после упорядочения информации. Зависимость здесь скорее линейная. Рассмотренные примеры иллюстрируют проблемы использования статистики DW для парной регрессии. Намного сложнее использовать эту статистику в случае множественной регрессии. По какой переменной упорядочивать информацию? И что отражает в этом случае статистика DW? Не всё так ясно. Для временных же рядов эти проблемы исчезают.
|
|||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 340. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. 2(1-
2(1-  ), где
), где  ), известном числе независимых переменных (m) и объёме выборки (n) (рисунок 3.6).
), известном числе независимых переменных (m) и объёме выборки (n) (рисунок 3.6).

 проверяет автокорреляцию только первого порядка;
проверяет автокорреляцию только первого порядка; , где n – объём выборки, а
, где n – объём выборки, а  – коэффициент множественной детерминации вспомогательного уравнения. Доказано, что если автокорреляция в остатках исходного уравнения отсутствует, то статистика
– коэффициент множественной детерминации вспомогательного уравнения. Доказано, что если автокорреляция в остатках исходного уравнения отсутствует, то статистика  (хи-квадрат распределению с p степенями свободы), где p – максимальное число лаговых значений остатков во вспомогательном уравнении. Если окажется, что
(хи-квадрат распределению с p степенями свободы), где p – максимальное число лаговых значений остатков во вспомогательном уравнении. Если окажется, что  , то гипотеза об отсутствии автокорреляции в остатках отклоняется.
, то гипотеза об отсутствии автокорреляции в остатках отклоняется. .
. .
. :
:  , против альтернативной гипотезы
, против альтернативной гипотезы 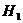 : не все
: не все  . После оценки вспомогательной регрессии проверяется неравенство
. После оценки вспомогательной регрессии проверяется неравенство