
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вывести условия параллельности, совпадения и перпендикулярности прямых на плоскости.Условие параллельности двух прямых (вывод): а) Если прямые
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е. Условия перпендикулярности двух прямых (вывод): а) Если прямые Таким образом, , необходимое и достаточное условие их перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку. б) Если уравнения прямых заданы в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, , то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A1A2 + B1B2 = 0. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 448. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  заданы уравнениями с угловым коэффициентом и параллельны, то
заданы уравнениями с угловым коэффициентом и параллельны, то 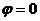 . Тогда
. Тогда 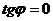 и из формулы
и из формулы 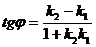
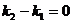 или
или 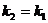 . Таким образом, достаточное условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.
. Таким образом, достаточное условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.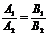 .
.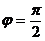 . Так как
. Так как 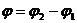 , то
, то 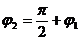 и
и 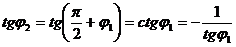 , т.е.
, т.е. 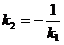 .
.