
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классификация точек разрыва функцииВсе точки разрыва функции разделяются на точки разрыва первого и второго рода. · Существуют левосторонний предел · Эти односторонние пределы конечны. При этом возможно следующие два случая: · Левосторонний предел и правосторонний предел равны друг другу:
Такая точка называется точкой устранимого разрыва. · Левосторонний предел и правосторонний предел не равны друг другу:
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов Пример. Рассмотрим функцию
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. Пример. Функция y=21/x непрерывна для всех значений x, кроме x=0. Найдем односторонние пределы:
Билет 13 ???????????? 1. Вывести формулу для вычисления расстояния от точки до плоскости. Пусть дана плоскость Выберем произвольную точку Вычитаем из первого соотношения второе получим Последнее соотношение представляет собой скалярное произведение нормального вектора плоскости и вектора 
Как вычисляется угол между плоскостями Пусть даны две плоскости Вывести условия параллельности и перпендикулярности двух плоскостей.?????? На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 462. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
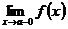 и правосторонний предел
и правосторонний предел 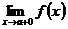 ;
;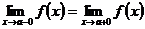 .
.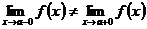
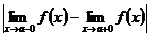 называется скачком функции.
называется скачком функции.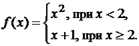
 многочлен).
многочлен). 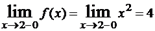 ,
, 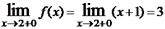 . Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что
. Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что 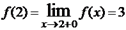 , следовательно функция в этой точке непрерывна справа (рис. 2).
, следовательно функция в этой точке непрерывна справа (рис. 2).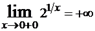 ,
, 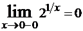 , следовательно x=0 – точка разрыва второго рода (рис. 3).
, следовательно x=0 – точка разрыва второго рода (рис. 3).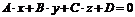 и точка
и точка 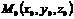 . Так как точка
. Так как точка 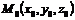 не лежит на плоскости, то
не лежит на плоскости, то 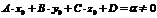 .
.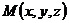 на плоскости. В этом случае имеем
на плоскости. В этом случае имеем 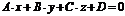 .
.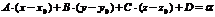
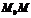 в координатной форме. По определению скалярного произведения имеем
в координатной форме. По определению скалярного произведения имеем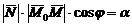 или
или 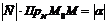 . Или окончательно
. Или окончательно 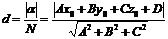
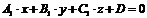 и
и 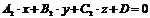 . Если они пересекаются, то угол между плоскостями определяется как угол между нормальными векторами этих плоскостей. Угол между двумя нормальными векторами определяется через скалярное произведение в координатной форме.
. Если они пересекаются, то угол между плоскостями определяется как угол между нормальными векторами этих плоскостей. Угол между двумя нормальными векторами определяется через скалярное произведение в координатной форме. 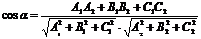 ,
, 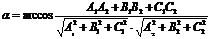 где
где 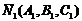 и
и 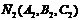 -нормальные векторы плоскостей.
-нормальные векторы плоскостей.