
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение прямой в отрезках на осях выводЕсли известны точки пересечения прямой с осями координатами В данном случае Из этого уравнения легко получаем Это и есть уравнение прямой в отрезках на осях: параметр Вывести канонические уравнения прямой на плоскости, Пусть
Запишем необходимое и достаточное условие коллинеарности векторов Если Полученное уравнение вида Записать параметрические уравнения, Уравнения системы Вывести уравнение прямой, проходящей через две заданные точки.??????? Выведем уравнение прямой a, которая в прямоугольной декартовой системе координат Oxy проходит через две несовпадающие точки Нам известно, что каноническое уравнение прямой на плоскости вида Напишем каноническое уравнение прямой a, проходящей через две заданные точки  Очевидно, направляющим вектором прямой a, которая проходит через точки М1 и М2, является вектор
2.Правила дифференцирования: доказать формулу Докажем правило дифференцирования произведения двух функций.
Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что
Что и требовалось доказать. перечислить остальные правила дифференцирования 1) При дифференцировании константу можно выносить за производную: 2) Правило дифференцирования суммы функций: 3) Правило дифференцирования разности функций: 4) Правило дифференцирования частного функций: 5) Правило дифференцирования функции в степени другой функции:
6) Правило дифференцирования сложной функции: 7) Правило логарифма при дифференцировании функции:
Билет 10 ???? 1. Угол между прямыми на плоскости, если они заданы каноническими уравнениями или уравнениями с угловым коэффициентом (вывод)????. Если прямые где Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами Вывод пусть даны:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 759. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  . Для этого воспользуемся уравнением прямой, проходящей через две точки
. Для этого воспользуемся уравнением прямой, проходящей через две точки  .
.
 -
- определяет точку пересечения прямой с осью
определяет точку пересечения прямой с осью  , параметр
, параметр  с осью
с осью  . Действительно, при х=0 получаем
. Действительно, при х=0 получаем  .
.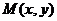 - плавающая точка прямой a. Тогда вектор
- плавающая точка прямой a. Тогда вектор  является направляющим вектором прямой a и имеет координаты
является направляющим вектором прямой a и имеет координаты  . Очевидно, что множество всех точек
. Очевидно, что множество всех точек  и имеющую направляющий вектор
и имеющую направляющий вектор  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 

 . Последнее равенство в координатной форме имеет вид
. Последнее равенство в координатной форме имеет вид 
 и
и  , то мы можем записать
, то мы можем записать
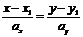 называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy.
называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy. называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy.
называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy. и
и  .
. задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку
задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку  .
.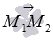 , он имеет координаты
, он имеет координаты  . Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора
. Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора 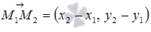 и координаты лежащей на ней точки
и координаты лежащей на ней точки  (или
(или  ).
).
 , перечислить остальные.
, перечислить остальные.

 и
и ,
,  (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
(приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
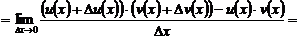



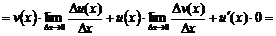

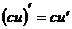


 ,
, 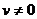
 ,
, 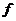 > 0
> 0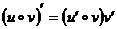
 ,
,  >0
>0 и
и  заданы каноническими уравнениями
заданы каноническими уравнениями  и
и  ,
, и
и  направляющие векторы прямых
направляющие векторы прямых  ,
, и
и 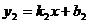 , вычисляется по формуле:
, вычисляется по формуле: 
 соответственно равны
соответственно равны  и
и  , тогда:
, тогда:  ,
, 