
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вывод общего уравнения прямой на плоскости.Теорема. Всякое уравнение первой степени вида Доказательство. Как видите, теорема состоит из двух частей. Докажем сначала, что уравнение вида Пусть координаты точки Уравнение
Таким образом, уравнение Теперь докажем, что всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку  На этом доказательство теоремы завершено. Уравнение вида Вывести уравнение прямой на плоскости с угловым коэффициентом и уравнение прямой в отрезках на осях. Уравнение прямой с угловым коэффициентом имеет вид Пусть прямая l не параллельна оси Оу (рис.1). Обозначим точку пересечения прямой l с осью Оу буквой В(О;в), а угол между положительным направлением оси Ох и прямой l обозначим угол, отсчитываемый от оси Ох против часовой стрелки ()
Выведем уравнение прямой l. Отсюда |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 631. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
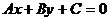 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида 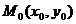 удовлетворяют уравнению
удовлетворяют уравнению 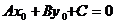 . Вычтем из левой и правой частей уравнения
. Вычтем из левой и правой частей уравнения 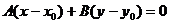 , которое эквивалентно
, которое эквивалентно 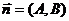 и
и  . То есть, множество всех точек
. То есть, множество всех точек 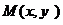 определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора
определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора  не были бы перпендикулярными и равенство
не были бы перпендикулярными и равенство 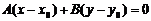 не выполнялось бы.
не выполнялось бы.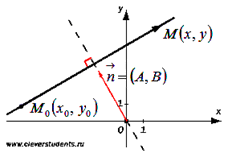
 перпендикулярны, следовательно, их скалярное произведение равно нулю, то есть,
перпендикулярны, следовательно, их скалярное произведение равно нулю, то есть,  . Полученное равенство можно переписать в виде
. Полученное равенство можно переписать в виде 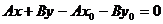 . Если принять
. Если принять 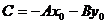 , то получим уравнение
, то получим уравнение 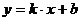 , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
, где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).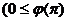 , называется углом наклона прямой l к оси Ох.
, называется углом наклона прямой l к оси Ох.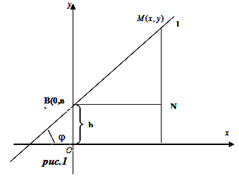
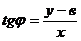 (1)
(1)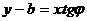 , или
, или 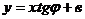 и окончательно
и окончательно 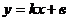 где
где 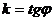 - Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
- Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.