
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Физический смысл векторного произведения
Свойства векторного произведения. 1. антикоммутативность 2. свойство дистрибутивности 3. сочетательное свойство Вычисление векторного произведения «в координатах» (с выводом). Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты Если разложить этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах: 2. Нахождение производной функции, заданной параметрически (с обоснованием). Вывод формулы производной параметрически заданной функции. Пусть Сначала переходим от параметрического задания к явному. При этом получаем сложную функцию Нахождение производной функции, заданной неявно (на примере). Если независимая переменная Несмотря на то, что уравнение  Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции. Пример. Найти производную неявной функции Решение. Производная неявно заданной функции всегда представляется в виде выражения, содержащего x и y: Разрешим полученное уравнение относительно производной:
Билет 8 1. Смешанное произведение векторов. Сме́шанное произведе́ние Его геометрический смысл. Если тройка векторов Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах Объем пирамиды, построенной на этой тройке векторов равен: Вычисление смешанного произведения через координаты векторов (вывод). Пусть заданы вектора: а = ахi + аyj + аzk , b = bхi + byj + bzk и с = схi + сyj + сzk Найдем их смешанное произведение, используя выражение в координатах для векторного и скалярного произведений:
Итак, Следовательно, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов. 2. Производная сложной функции, производная обратной функции (с доказательствами). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 863. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

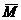 -момент силы
-момент силы  относительно тоски О;
относительно тоски О;  -радиус-вектор точки приложения силы
-радиус-вектор точки приложения силы  причем если перенести
причем если перенести  ,
,  ;
; или
или  ;
; или
или  , где
, где  - произвольное действительное число.
- произвольное действительное число. ,
,  ,
,  , во второй строке находятся координаты вектора
, во второй строке находятся координаты вектора  , а в третьей – координаты вектора
, а в третьей – координаты вектора  в заданной прямоугольной системе координат:
в заданной прямоугольной системе координат:

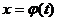 ,
,  определены и дифференцируемы при
определены и дифференцируемы при  , причем
, причем  и
и  имеет обратную функцию
имеет обратную функцию 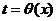 .
. , аргументом которой является x. По правилу нахождения производной сложной функции имеем:
, аргументом которой является x. По правилу нахождения производной сложной функции имеем:  . Так как
. Так как 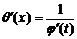 , поэтому
, поэтому 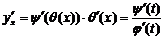
 и функция
и функция  связаны уравнением вида
связаны уравнением вида  , которое не разрешено относительно
, которое не разрешено относительно  .
. .
.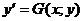 . Чтобы прийти к такому результату, продифференцируем обе части равенства:
. Чтобы прийти к такому результату, продифференцируем обе части равенства:

 векторов —скалярное произведение вектора
векторов —скалярное произведение вектора  на векторное произведение векторов
на векторное произведение векторов  и
и  :
:  .
. правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:  . В случае левой тройки
. В случае левой тройки  . Если
. Если  ,
, 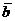 и
и  компланарны, то их смешанное произведение равно нулю.
компланарны, то их смешанное произведение равно нулю.
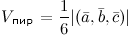

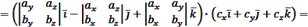
 .
.
 .
.