
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление скалярного произведения через координаты (вывод).Пусть заданы два вектора Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат Условие перпендикулярности двух векторов в векторной и координатной формах. - Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. - Даны два вектора
2. Дифференциал: определение, геометрическая интерпретация, применение к приближенным вычислениям. Дифференциалом функции называется линейная часть приращения функции относительно приращения аргумента Δ f = A·Δx + o(Δx), то есть df = A·Δx. Геометрический смысл дифференциала
Возьмем на графике некоторую точку Геометрический смысл: значение дифференциала функции при данном значении аргумента Замечание. Из определения дифференциала следует, что производная функции равна отношению дифференциала функции к дифференциалу ее аргумента  Применение дифференциала в приближенных вычислениях Абсолютной погрешностью приближенной величины Отсюда Относительная погрешность – это отношение абсолютной погрешности Границей относительной погрешности Для этого воспользуемся приближенным равенством Но Показано, что абсолютная погрешность не превышает Для приближенного вычисления значения функции применяется следующая формула:
Билет 7 1. Векторное произведение двух векторов и его физический смысл. Векторным произведением двух векторов |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 448. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и 
 ,
, 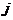 ,
,  :
:



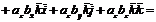

 и
и  . Эти векторы будут перпендикулярны, если выражение
. Эти векторы будут перпендикулярны, если выражение  на плоскости, а в трехмерном пространстве
на плоскости, а в трехмерном пространстве  .
.
 и другую точку
и другую точку  , абсцисса которой
, абсцисса которой  . Проведем касательную
. Проведем касательную  к графику функции в точке
к графику функции в точке  . А из треугольника KMN известно, что
. А из треугольника KMN известно, что  . Итак
. Итак 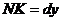
 и данном приращении
и данном приращении  равно приращению ординаты касательной, проведенной в точке с абсциссой
равно приращению ординаты касательной, проведенной в точке с абсциссой 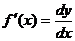 .
. называется абсолютная величина разности между точным значением этой величины
называется абсолютная величина разности между точным значением этой величины  и её приближенным значением
и её приближенным значением  . Границей абсолютной погрешности приближенной величины
. Границей абсолютной погрешности приближенной величины  , не меньше
, не меньше  :
:  .
.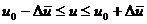 . Чем меньше
. Чем меньше  .
. называется отношение
называется отношение  . При этом
. При этом  и
и 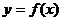 и её производной в точке
и её производной в точке  .
. или
или  .
. , поэтому
, поэтому  , откуда
, откуда 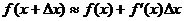 .
. , где
, где  на сегменте
на сегменте  .
.

 и
и  , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор
, заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор 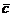 , что
, что