
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Декартовая прямоугольная система координат.Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY - осью ординат (третья ось OZ - осью аппликат). Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел - координат данной точки. Левая и правая системы координат.
Декартовая прямоугольная система координат Охуz называется правой,если тройка её базисных векторов В основном используют правые прямоугольные системы координа Координаты вектора – коэффициенты его разложения в ортогональном базисе.
Формула Коэффициенты разложения – проекции на оси координат. Из рисунка видно, что коэффициенты разложения-координаты вектора (  Радиус – вектор точки. - это вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой. Длина вектора «в координатах». формула для нахождения длины вектора Направление вектора. Направлением вектора считается направление от его начала к его концу «Направляющие» косинусы и зависимость между ними. Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат. Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам. Если в пространстве задан вектор Здесь Сумма квадратов направляющих косинусов равна единице:
2. Формула Лангража конечных приращений. Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция Правило Лопиталя (вывод). Теорема Лопиталя: Если:
то существует Пределы также могут быть односторонними. Или Теорема 5.5 (Правило Лопиталя) Пусть функции Доказательство. Заметим, что из условия Пусть Перейдём теперь в этом равенстве к пределу при так как, очевидно, при Переходя к пределу при так как при Итак, оба односторонних предела отношения Примеры его применения. Задание. Найти Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.
Ответ. Задание. Найти Решение. Получим неопределенность не подходящую под правило Лопиталя, приведем ее к нужному виду и для решения предела воспользуемся правилом Лопиталя.
Ответ.
Билет 6 1. Скалярное произведение векторов. Скалярным произведением двух векторов Его физический смысл. Пусть материальная точка перемещается под действием постоянной силы
На рисунке 1 сила С другой стороны, Свойства скалярного произведения. Для любых векторов 1) a · b = b · a -свойство перестановки (коммутативности): (от перестановки множителей скалярное произведение не меняется); 2) a · (b · c) = (a · b) · c -свойство распределения: (результат не зависит от порядка умножения); 3) a(b+c)=ab+ac - свойство дистрибутивности 4) (λ a) · b = λ (a · b) - свойство сочетания (по отношению к скалярному множителю): 5) Свойство ортогональности (перпендикулярности): если вектора a и b ненулевые, то их скалярное произведение равно нулю, только когда эти векторы ортогональны (перпендикулярны друг к другу) 6) a · a = a2 = |a|2 - свойство квадрата (скалярное произведения вектора самого с собой равняется квадрату его модуля); 7) Для доказательства координаты векторов: |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 514. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Три некомпланарных вектора
Три некомпланарных вектора  ,
,  ,
, 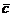 , взятых в указанном порядке называют тройкой векторов. Пусть векторы
, взятых в указанном порядке называют тройкой векторов. Пусть векторы  является правой, и левой,если тройка
является правой, и левой,если тройка  Любой вектор
Любой вектор  может быть представлен в виде линейной комбинации тройки взаимно перпендикулярных (ортогональных) векторов
может быть представлен в виде линейной комбинации тройки взаимно перпендикулярных (ортогональных) векторов  :
:
 выражает разложение вектора
выражает разложение вектора  по ортогональному базису
по ортогональному базису  являются коэффициентами разложения вектора в ортогональном базисе.
являются коэффициентами разложения вектора в ортогональном базисе. по его координатам на плоскости имеет вид
по его координатам на плоскости имеет вид  , длина вектора
, длина вектора  в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле
в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле  .
. , то его направляющие косинусы вычисляются по формулам:
, то его направляющие косинусы вычисляются по формулам:  ,
,  ,
, 
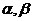 и
и  - углы, которые составляет вектор с положительными направлениями осей Ox, Oy и Oz соответственно.
- углы, которые составляет вектор с положительными направлениями осей Ox, Oy и Oz соответственно.
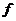 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в интервале
и дифференцируема в интервале  , то найдётся такая точка
, то найдётся такая точка  , что
, что  .
.
 ;
; и
и  дифференцируемы в окрестности
дифференцируемы в окрестности  ;
; в окрестности
в окрестности  ,
, .
. и
и  непрерывны в некоторой окрестности
непрерывны в некоторой окрестности  точки
точки  и
и 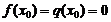 , то есть
, то есть  и
и  при
при 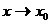 . Предположим, что при
. Предположим, что при 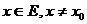 функции
функции  и
и  , причём существует предел отношения этих производных:
, причём существует предел отношения этих производных:  . Тогда предел отношения самих функций
. Тогда предел отношения самих функций 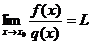
 следует, что оба односторонних предела также равны L:
следует, что оба односторонних предела также равны L:  и
и 
 ,
,  . По теореме Коши, применённой к отрезку
. По теореме Коши, применённой к отрезку  , получим тогда, с учётом того, что
, получим тогда, с учётом того, что  ,
,  ,
,  , где
, где 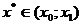 .
.  :
:  ,
, . Теперь возьмём точку
. Теперь возьмём точку 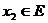 ,
,  и применим теорему Коши к отрезку
и применим теорему Коши к отрезку  . Получим :
. Получим :  , где
, где 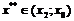 .
.  , получаем
, получаем  ,
, .
.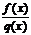 равны L. На основании теоремы о связи односторонних пределов с двусторонним получаем, что
равны L. На основании теоремы о связи односторонних пределов с двусторонним получаем, что 



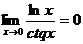



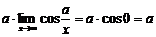


 вдоль вектора перемещения
вдоль вектора перемещения  .
.
 разложена на две ортогональные составляющие
разложена на две ортогональные составляющие  и
и 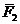 , причем, из физики нам известно, что работа при перемещении материальной точки вдоль вектора
, причем, из физики нам известно, что работа при перемещении материальной точки вдоль вектора  .
.  , откуда получаем:
, откуда получаем: 
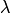 :
:
 ;
;  ,
,  ,
, 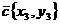 подставляются в формулу произведения
подставляются в формулу произведения 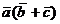 . После подстановки координат получается выражение
. После подстановки координат получается выражение  , которое и соответствует сумме скалярных произведений
, которое и соответствует сумме скалярных произведений  .
.