
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналогично для наибольших нижних граней.Д о к а з а т е л ь с т в о. В самом деле, Поэтому Неравенство в теореме 6 нельзя заменить равенством даже в случае полных решеток Брауэра. Вместе с тем вернее Теорема 7. Если Д о к а з а т е л ь с т в о. Т.к. Наконец, для булевых колец верна теория де Моргана. Теорема 8. Если существует наименьшая верхняя грань Д о к а з а т е л ь с т в о. Т.к.
Приведенный выше анализ показывает, что все основные теоремы §1 можно обобщить на случаи полных булевых колец. Для неполных колец эти теоремы верны при условии, что все верхние и нижние грани, встречающиеся в условиях теоремы, существуют. Интересно отметить, что, хотя в законе дистрибутивности не содержится знака дополнения (теорема 7), он выполняется только для булевых колец. Еще более интересно складываются обстоятельства для обобщенного закона дистрибутивности (теорема 4, § 1). Мы покажем, что булевы кольца вида Сначала дадим два определения. О п р е д е л е н и е 1. Булево кольцо 
где О п р е д е л е н и е 2. Элемент Теорема 9. Каждое полное и атомарное кольцо
для любого множества Д о к а з а т е л ь с т в о. Обозначим Функция 1) 2) следует, что 1) и 3) Из равенств 1), 3) следует, что Т.е. Равенства 2), 4) дают:
Таким образом, или 1) и 4); или 2) и 3). В первом случае ( 1) и 4) ) Значит, или или Но в обоих этих случаях Пусть Итак, мы доказали, что прямое включение из (3) справедливо:
Пусть теперь Итак, обратное включение Еще проще доказывается равенство (4) Тогда в соответствии с (3) Теорема 9 доказана полностью. Теорема 10. Полное атомарное булево кольцо Д о к а з а т е л ь с т в о. Согласно теореме 9 , существует функция |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 267. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
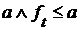 и
и 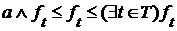 для любого
для любого 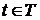 .
.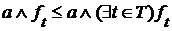 , откуда следует утверждение теоремы.
, откуда следует утверждение теоремы.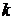 - булево кольцо и существует наименьшая верхняя грань
- булево кольцо и существует наименьшая верхняя грань 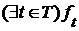 , то для произвольного
, то для произвольного 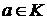 существует наименьшая верхняя грань
существует наименьшая верхняя грань 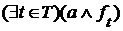 и она равна
и она равна 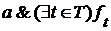 . Аналогично для наибольшей нижней грани.
. Аналогично для наибольшей нижней грани.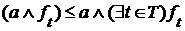 для каждого
для каждого 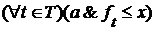 , то
, то 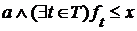 . Из условия следует, что
. Из условия следует, что 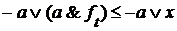 , поэтому
, поэтому 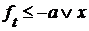 для произвольного
для произвольного 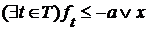 , следовательно,
, следовательно, 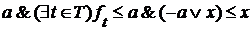 .
.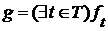 , то существует грань
, то существует грань 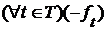 и она равна
и она равна 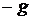 . Аналогично для наибольшей нижней грани.
. Аналогично для наибольшей нижней грани.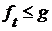 , то, по закону контрапозиции,
, то, по закону контрапозиции, 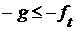 для каждого
для каждого 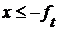 для каждого
для каждого 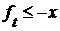 , а поэтому
, а поэтому 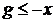 и
и 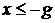 , откуда
, откуда 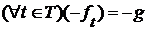 .
.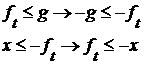
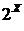 являются в принципе единственными булевыми кольцами, для которых этот закон выполняется.
являются в принципе единственными булевыми кольцами, для которых этот закон выполняется.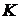 называется дистрибутивным, если оно полно и для каждого множества
называется дистрибутивным, если оно полно и для каждого множества 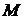 , каждой функции
, каждой функции 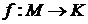 и каждого разбиения
и каждого разбиения 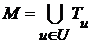 на сумму непустых множеств
на сумму непустых множеств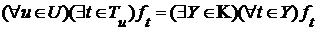 (1)
(1)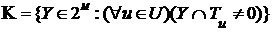 (2).
(2).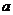 называется атомом булева кольца
называется атомом булева кольца 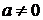 и
и  . Кольцо
. Кольцо 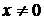 существует по крайней мере один такой атом
существует по крайней мере один такой атом 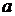 , что
, что 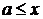 .
.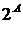 всех подмножеств множества
всех подмножеств множества 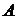 его атомов, а именно существует такое взаимно однозначное отображение
его атомов, а именно существует такое взаимно однозначное отображение  множества
множества 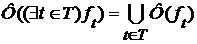 (3),
(3),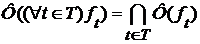 (4)
(4)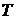 и любой функции
и любой функции 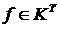 .
.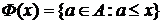 ,
, 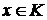 . Эта формула задает функцию, определенную на
. Эта формула задает функцию, определенную на 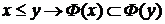 .
.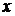 и
и 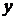 - элементы кольца
- элементы кольца 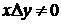 т.к. кольцо атомарно, то существует такой атом
т.к. кольцо атомарно, то существует такой атом 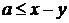 . Из неравенств
. Из неравенств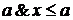 ,
,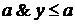
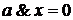 или 2)
или 2) 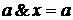
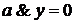 или 4)
или 4) 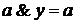 .
.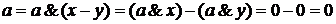 .
.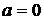 , что противоречит определению 2.
, что противоречит определению 2.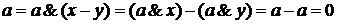 , что противоречит определению 2.
, что противоречит определению 2.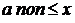 и
и 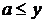 , во втором случае ( 2) и 3) )
, во втором случае ( 2) и 3) ) 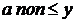 .
.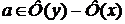 ,
,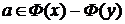 .
.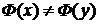 .
.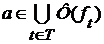 , то существует такое
, то существует такое 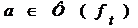 , откуда
, откуда  , а поэтому
, а поэтому 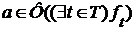 .
.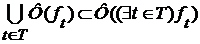 (5).
(5).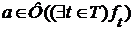 , т.е.
, т.е. 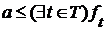 . Если
. Если 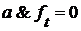 для каждого
для каждого  , то
, то 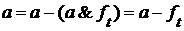 , и, значит :
, и, значит : 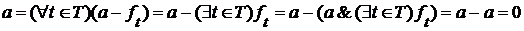 , т.к.
, т.к. 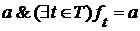 . Но это противоречит тому, что
. Но это противоречит тому, что 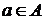 . Следовательно, существует такое
. Следовательно, существует такое 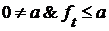 , т.е.
, т.е. 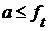 , а поэтому
, а поэтому 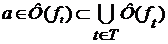 .
.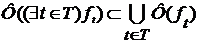 доказано. Оно вместе с (5) дает равенство (3).
доказано. Оно вместе с (5) дает равенство (3).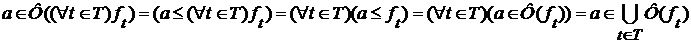 Осталось показать, что каждое множество
Осталось показать, что каждое множество 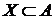 можно представить в виде
можно представить в виде 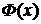 для некоторого
для некоторого 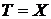 ,
, 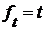 ,
, 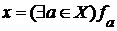 ( эта
( эта 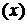 - наименьшая верхняя грань существует, т.к. кольцо
- наименьшая верхняя грань существует, т.к. кольцо 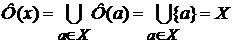 , поскольку
, поскольку 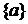 , а значит,
, а значит, 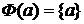 .
.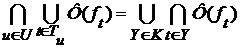 , откуда в силу (3) и (4)
, откуда в силу (3) и (4) 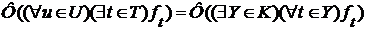 . Т.к. функция
. Т.к. функция