Декартовы произведения топологических пространств.
Пусть 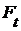 для каждого t для каждого t 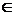 T является топологическим пространством. Обозначим через T является топологическим пространством. Обозначим через 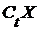 замыкание в пространстве замыкание в пространстве 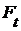 множества множества 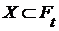 . Таким образом, . Таким образом,  – такая функция, что – такая функция, что 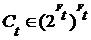 для каждого t. для каждого t.
Очевидно, что существует много способов определения замыкания в пространстве 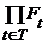 , т.к. каждое множество можно превратить в топологическое пространство разными способами. , т.к. каждое множество можно превратить в топологическое пространство разными способами.
Опишем здесь некоторую специальную топологию пространства 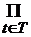 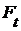 , введенную Тихоновым. , введенную Тихоновым.
Пусть 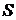 - конечное подмножество множества T, а - конечное подмножество множества T, а 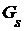 - открытое множество в пространстве - открытое множество в пространстве 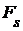 для каждого для каждого 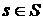 . Назовем окрестностью, определяемой множеством . Назовем окрестностью, определяемой множеством 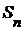 покрытыми множествами покрытыми множествами 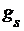 , подмножество , подмножество 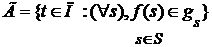 декартова произведения декартова произведения 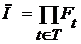 . .
Докажем, что произведение двух окрестностей либо пусто, либо тоже окрестность. В самом деле, если окрестность Г определена конечными множествами S и открытыми множествами  , а окрестность , а окрестность 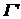 определена конечными множествами определена конечными множествами 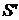 и открытыми множествами и открытыми множествами 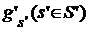 , то , то 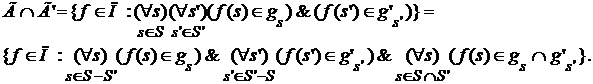
Таким образом, множество  , либо пусто, либо является окрестностью, определяемым конечным множеством , либо пусто, либо является окрестностью, определяемым конечным множеством  и открытыми множествами. и открытыми множествами.
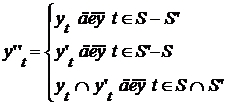
Определим замыкание множества 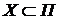 как множество CX таких как множество CX таких 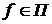 , что каждая окружность , что каждая окружность 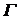 , содержащая , содержащая  , содержит по крайней мере один элемент множества , содержит по крайней мере один элемент множества  : :
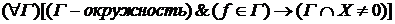 (*) (*)
Теорема 1. Декартово произведение 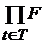 представляет собой топологическое пространство относительно операции замыкания представляет собой топологическое пространство относительно операции замыкания  для для 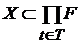 . .
Д о к а з а т е л ь с т в о. Для доказательства теоремы проверим, выполняются ли аксиомы (1)-(4) (гл. I , § 8). Аксиомы (3), (4) очевидны :
Аксиома (3) :  ; аксиома (4): ; аксиома (4): 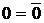 . .
Аксиома 1. 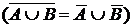 Пусть Пусть 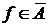 . Тогда каждая окрестность, содержащая . Тогда каждая окрестность, содержащая  , содержит хотя бы один элемент из , содержит хотя бы один элемент из 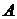 . Значит, . Значит, 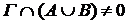 , а отсюда следует, что , а отсюда следует, что 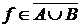 , и тогда , и тогда 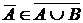 . Аналогично . Аналогично 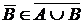 , следовательно, , следовательно, 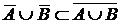 . .
Пусть теперь 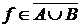 , , 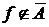 . Тогда . Тогда 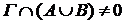 для каждой окрестности Г, содержащей f , и для каждой окрестности Г, содержащей f , и 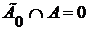 для некоторой окрестности для некоторой окрестности 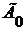 , содержащей f . Если Г – правильная окрестность, содержащая f , то , содержащей f . Если Г – правильная окрестность, содержащая f , то 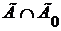 - также окрестность, содержащая f , и поэтому - также окрестность, содержащая f , и поэтому 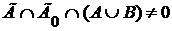 , откуда , откуда 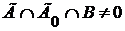 и тем более и тем более 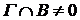 . Это значит, что . Это значит, что 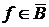 . .
Аксиома 2. ( 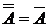 ). Достаточно показать, что ). Достаточно показать, что 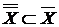 . Пусть . Пусть 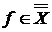 и Г – производная окрестность, содержащая f. Следовательно, и Г – производная окрестность, содержащая f. Следовательно, 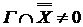 . Возьмем . Возьмем 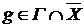 . Тогда Г – окрестность, содержащая g , и т.к. . Тогда Г – окрестность, содержащая g , и т.к.  , то , то  . Это значит, что выполняется условие (*) , и поэтому . Это значит, что выполняется условие (*) , и поэтому 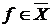 . .
Приведем примеры декартовых произведений топологических пространств.
Пример 1. Множество Кантора. Так называется множество 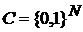 , т.е. декартова степень двухэлементного множества. , т.е. декартова степень двухэлементного множества.
Если в множестве 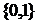 определить топологию, положив определить топологию, положив 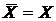 для каждого для каждого  (дискретная топология), то (дискретная топология), то  станет топологическом пространством с топологией Тихонова. станет топологическом пространством с топологией Тихонова.
Ставя в соответствие элементу 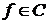 вещественное число вещественное число 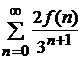 , получаем взаимно однозначное соответствие , получаем взаимно однозначное соответствие 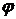 множества множества  и множества вещественных чисел замкнутого интервала и множества вещественных чисел замкнутого интервала 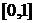 , имеющих в топологическом разложении только цифры 0 и 2. , имеющих в топологическом разложении только цифры 0 и 2.
Пример 2. Обобщенное множество Кантора 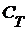 . Это декартова степень . Это декартова степень 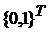 . Топология Тихонова в этом множестве определяется так же, как для множества . Топология Тихонова в этом множестве определяется так же, как для множества  . .
Обобщенное множество Кантора можно также определить как множество характеристических функций подмножеств множества 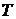 . В действительности можно отождествить множества . В действительности можно отождествить множества 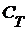 и и 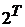 . Поэтому в дальнейшем не будем трактовать множество . Поэтому в дальнейшем не будем трактовать множество 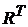 как топологическое пространство. Аналогично можно отождествить элементы множества как топологическое пространство. Аналогично можно отождествить элементы множества 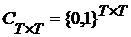 с отношениями над полями, содержащимися в с отношениями над полями, содержащимися в 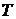 , поскольку каждый элемент множества , поскольку каждый элемент множества 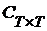 является характеристической функцией множества упорядоченных пар элементов из является характеристической функцией множества упорядоченных пар элементов из 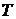 . .
Tеорема 2. Семейство 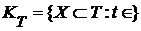 замкнуто и открыто в замкнуто и открыто в 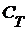 . Семейство . Семейство 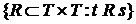 замкнуто и открыто в замкнуто и открыто в 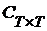 . .
Д о к а з а т е л ь с т в о. Обозначим через 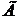 окрестность в окрестность в 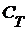 , определенную множеством , определенную множеством 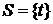 и открытым множеством и открытым множеством 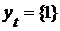 . Тогда . Тогда 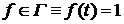 и, значит, и, значит, 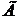 состоит из характеристических функций множеств, принадлежащих семейству состоит из характеристических функций множеств, принадлежащих семейству 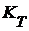 . Таким образом, . Таким образом, 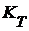 - открытое множество. Аналогично окрестность, определенная множеством - открытое множество. Аналогично окрестность, определенная множеством 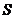 и открытым множеством и открытым множеством 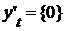 , состоит из характеристических функций множеств, составляющих семейство , состоит из характеристических функций множеств, составляющих семейство 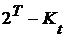 . Эта доказывает, что семейство . Эта доказывает, что семейство 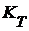 замкнуто в замкнуто в 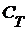 . .
Вторая часть теоремы следует из первой.
Пример 3. Пространство Бэра. Так называется декартова степень 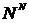 , т.е. множество бесконечных последовательностей натуральных чисел. Топология в , т.е. множество бесконечных последовательностей натуральных чисел. Топология в 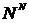 - топология Тихонова, при чем операция замыкания в - топология Тихонова, при чем операция замыкания в 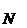 определяется равенством определяется равенством 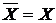 . .
Если  - последовательность из - последовательность из  членов членов 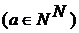 , то множество , то множество 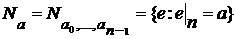 одновременно замкнуто и открыто в одновременно замкнуто и открыто в 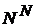 . .
Это множество последовательностей  , удовлетворяющих условиям , удовлетворяющих условиям  для для 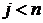 , т.е. оно совпадает окрестностью , т.е. оно совпадает окрестностью 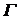 в в 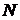 , определенной множеством , определенной множеством 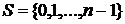 и открытыми множествами и открытыми множествами 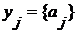 для для 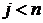 . .
Дополнение этой окрестности открыто 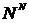 , т.к. оно совпадает с суммой окрестностей, определенных множествами , т.к. оно совпадает с суммой окрестностей, определенных множествами 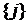 и открытыми множествами и открытыми множествами 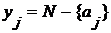 , , 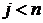 . .
Ставя в соответствие элементу  число число 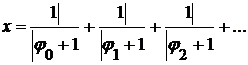 , ,
Получим взаимно однозначные отображения пространства 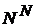 на множество иррациональных чисел открытого интервала (0,1). на множество иррациональных чисел открытого интервала (0,1).
Таким образом, можно отождествить пространство Бэра с множеством иррациональных чисел, удовлетворяющих условию  . .
Пример 4. Декартово произведение конечного числа пространств. Конструкция, описанная в этом параграфе, в одинаковой степени применима как к случаю, когда множество 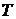 в формуле в формуле 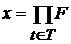 конечно, так и к случаю, когда это множество бесконечно. конечно, так и к случаю, когда это множество бесконечно.
Если 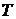 - конечное множество, например - конечное множество, например 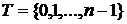 , то декартово произведение , то декартово произведение 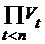 , где для каждого , где для каждого  множество множество 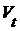 открыто в открыто в 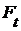 , образует открытую базу в , образует открытую базу в 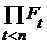 . .
Если 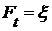 , где , где  - множество вещественных чисел, то пространство - множество вещественных чисел, то пространство  называется n-мерным евклидовым пространством. Это пространство мы будем применять в дальнейшем только в некоторых примерах, т.к. в отличие от других рассмотренных выше пространств оно было определено не только с помощью понятий теории множеств. называется n-мерным евклидовым пространством. Это пространство мы будем применять в дальнейшем только в некоторых примерах, т.к. в отличие от других рассмотренных выше пространств оно было определено не только с помощью понятий теории множеств.
В дальнейших главах мы будем пользоваться следующей теоремой.
Теорема 3. Если 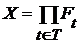 - декартово произведение топологических пространств (с топологией Тихонова), - декартово произведение топологических пространств (с топологией Тихонова), 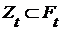 , , 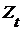 для каждого для каждого 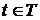 замкнуто в замкнуто в 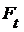 , то , то 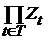 также замкнуто. также замкнуто.
Д о к а з а т е л ь с т в о. Пусть 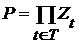 и и 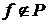 . Тогда . Тогда 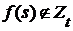 для некоторого для некоторого 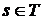 . Окрестность . Окрестность 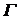 точки точки  , определенная одноэлементным множеством , определенная одноэлементным множеством 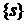 и открытым множеством и открытым множеством 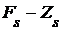 , содержит , содержит  и не пересекается с и не пересекается с 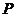 , что и т.д. , что и т.д.
Теорема Тихонова.
Семейство R подмножеств множества  называется центрированным, если пересечение любого конечного числа множеств из R не пусто, т.е. существует «центр».(НК) называется центрированным, если пересечение любого конечного числа множеств из R не пусто, т.е. существует «центр».(НК)
Топологическое пространство  называется компактным, если каждое центрированное семейство его замкнутых подмножеств имеет непустое пересечение. Это значит, что топологическое пространство называется компактным, если каждое центрированное семейство его замкнутых подмножеств имеет непустое пересечение. Это значит, что топологическое пространство  компактно тогда и только тогда, когда каждое семейство открытых множеств, в сумме составляющих компактно тогда и только тогда, когда каждое семейство открытых множеств, в сумме составляющих  , содержит конечное подмножество, сумма множеств которого также равна , содержит конечное подмножество, сумма множеств которого также равна  . .
Приведенная ниже теорема относится, собственно говоря, не к общей теории множеств, а к топологии.
Мы ее поместили здесь потому, что она имеет многочисленные приложения(между прочим, и в самой теории множеств), методы, применяемые в ее доказательстве, фактически не выводят нас из теории множеств.
°Теорема 1 (Тихонов). Если для каждого 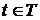 пространство пространство  компактно, то пространство компактно, то пространство 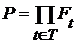 также компактно (в топологии Тихонова). также компактно (в топологии Тихонова).
При доказательстве этой теоремы мы будем пользоваться леммой, которую докажем только в главе 7, § 8.
°Лемма. Если R0 - центрированное семейство подмножеств пространства  , то существует максимальное центрированное семейство R , то существует максимальное центрированное семейство R 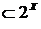 , содержащее R0, т.е. такое, что каждое семейство подмножеств пространства , содержащее R0, т.е. такое, что каждое семейство подмножеств пространства  , отличное от R и содержащее R0, содержит конечное подсемейство, имеющее пустое пересечение. , отличное от R и содержащее R0, содержит конечное подсемейство, имеющее пустое пересечение.
Воспользуемся следующими двумя свойствами центрированных максимальных семейств.
I. Если 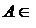 R и R и 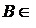 R, то R, то 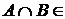 R. R.
В самом деле, в противном случае семейство, полученное из R прибавлением к нему 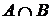 , не было бы центрированным, и, значит, содержало бы конечное подсемейство с пустым пересечением. Очевидно, что множество , не было бы центрированным, и, значит, содержало бы конечное подсемейство с пустым пересечением. Очевидно, что множество 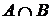 должно принадлежать этому подсемейству, а отсюда следует, что существует такое конечное подсемейство R' должно принадлежать этому подсемейству, а отсюда следует, что существует такое конечное подсемейство R' 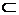 R, что R, что 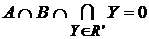 , что противоречит центрированности семейства R. , что противоречит центрированности семейства R.
II. Если 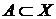 и и 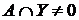 для каждого для каждого 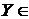 R, то R, то 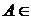 R. В самом деле, в противном случае семейство R R. В самом деле, в противном случае семейство R  не было бы центрированным и, значит, существовало бы такое конечное подсемейство R' не было бы центрированным и, значит, существовало бы такое конечное подсемейство R' 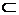 R, что R, что 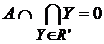 . В силу свойства I произведение . В силу свойства I произведение 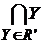 принадлежит R, вопреки тому, что принадлежит R, вопреки тому, что 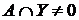 для каждого для каждого 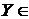 R. R.
Д о к а з а т е л ь с т в о теоремы Тихонова. Пусть R0 теперь - центрированное семейство замкнутых подмножеств пространства 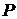 . Обозначим через Rнекоторое центрированное максимальное семейство подмножеств пространства . Обозначим через Rнекоторое центрированное максимальное семейство подмножеств пространства 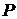 , содержащее R0. Для доказательства теоремы достаточно показать, что , содержащее R0. Для доказательства теоремы достаточно показать, что 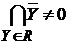 . .
Для произвольного множества 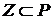 обозначим через обозначим через 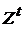 его проекцию на его проекцию на 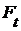 и положим Rt и положим Rt  R}. Семейство Rt состоит из замкнутых подмножеств пространства R}. Семейство Rt состоит из замкнутых подмножеств пространства 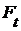 . Если множества . Если множества 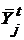 , , 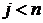 , принадлежит Rt, при чем , принадлежит Rt, при чем  R, то R, то  , т.к. семейство R центрировано. Отсюда следует, что , т.к. семейство R центрировано. Отсюда следует, что 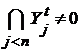 и тем более и тем более 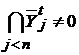 . .
Значит, семейство Rt центрировано. Т.к. все 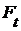 контактны, то контактны, то 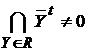 . Использую общий принцип выбора, получаем отсюда, что существует такая функция . Использую общий принцип выбора, получаем отсюда, что существует такая функция 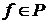 , что , что 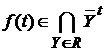 для каждого для каждого 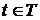 . Докажем, что . Докажем, что 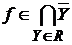 . .
Для этого возьмем множество  из R и окрестность из R и окрестность 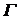 , содержащую , содержащую  . Надо показать, что . Надо показать, что 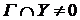 . .
Пусть 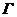 определяется конечным множеством определяется конечным множеством 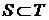 и открытыми множествами и открытыми множествами 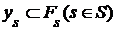 . .
Очевидно, что 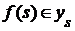 для для 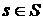 . Полагая . Полагая 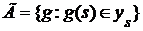 , получим , получим 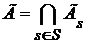 . .
Если 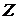 - произвольное множество из R, то - произвольное множество из R, то 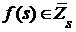 , следовательно, , следовательно, 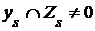 . Поэтому существует такой элемент . Поэтому существует такой элемент 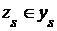 , что , что 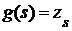 для некоторой функции для некоторой функции 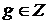 и, значит, и, значит, 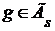 . Таким образом, . Таким образом, 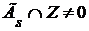 для любого для любого 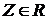 . Отсюда, согласно (II) получаем . Отсюда, согласно (II) получаем 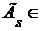 R, а согласно (I), R, а согласно (I), 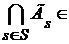 R, т.е. R, т.е. 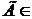 R, откуда R, откуда 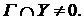 Таким образом, любая окрестность, содержащая Таким образом, любая окрестность, содержащая 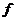 , имеет общие элементы с , имеет общие элементы с 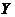 , значит, , значит, 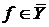 . .
Пример 1. Множества  , ,  , , 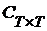 компактны. компактны.
Пример 2. Пусть 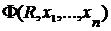 - высказывательная функция, полученная из высказывательных функций - высказывательная функция, полученная из высказывательных функций
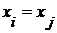 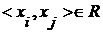 (*) (*)
с помощью одних только операций исчисления высказываний. Также высказывательные функции назовем открытыми.
Пусть 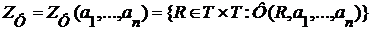 для для 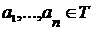 и произвольной открытой высказывательной функции и произвольной открытой высказывательной функции  . .
Множество 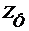 одновременно открыто и замкнуто в одновременно открыто и замкнуто в 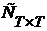 . Действительно, для высказывательных функций (*) это следует из теоремы 2 (§ 6), а для других высказывательных функций – из связи между логическими теоретико-множественными операциями и просто замечания, что сумма, произведение и дополнение открыто-замкнутых множеств тоже открыты и замкнуты. . Действительно, для высказывательных функций (*) это следует из теоремы 2 (§ 6), а для других высказывательных функций – из связи между логическими теоретико-множественными операциями и просто замечания, что сумма, произведение и дополнение открыто-замкнутых множеств тоже открыты и замкнуты.
Пусть теперь 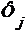 - открытая высказывательная функция с переменными - открытая высказывательная функция с переменными 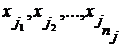 , и пусть , и пусть 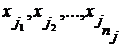 - элементы множества - элементы множества  . Из компактности множества . Из компактности множества 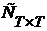 следует следует
Теорема 2. Если для каждого 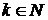 произведение произведение 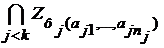 не пусто, то и бесконечное произведение не пусто, то и бесконечное произведение 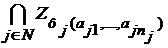 непусто. непусто.
В этой теореме утверждается, что из существования отношений 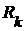 , удовлетворяющих условиям , удовлетворяющих условиям 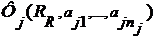 для для 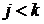 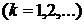 , следует существование одного “универсального” отношения, удовлетворяющего всем этим условиям. , следует существование одного “универсального” отношения, удовлетворяющего всем этим условиям.
|


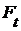 для каждого t
для каждого t 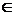 T является топологическим пространством. Обозначим через
T является топологическим пространством. Обозначим через 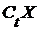 замыкание в пространстве
замыкание в пространстве 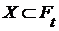 . Таким образом,
. Таким образом,  – такая функция, что
– такая функция, что 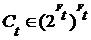 для каждого t.
для каждого t.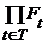 , т.к. каждое множество можно превратить в топологическое пространство разными способами.
, т.к. каждое множество можно превратить в топологическое пространство разными способами.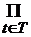
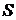 - конечное подмножество множества T, а
- конечное подмножество множества T, а 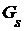 - открытое множество в пространстве
- открытое множество в пространстве 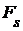 для каждого
для каждого 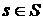 . Назовем окрестностью, определяемой множеством
. Назовем окрестностью, определяемой множеством 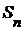 покрытыми множествами
покрытыми множествами 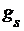 , подмножество
, подмножество 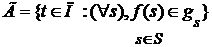 декартова произведения
декартова произведения 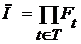 .
. , а окрестность
, а окрестность 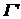 определена конечными множествами
определена конечными множествами 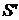 и открытыми множествами
и открытыми множествами 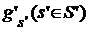 , то
, то 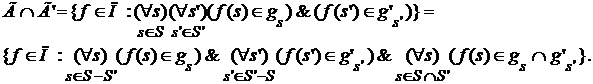
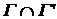 , либо пусто, либо является окрестностью, определяемым конечным множеством
, либо пусто, либо является окрестностью, определяемым конечным множеством  и открытыми множествами.
и открытыми множествами.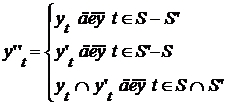
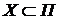 как множество CX таких
как множество CX таких 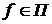 , что каждая окружность
, что каждая окружность 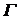 , содержащая
, содержащая  , содержит по крайней мере один элемент множества
, содержит по крайней мере один элемент множества  :
: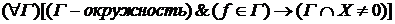 (*)
(*)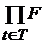 представляет собой топологическое пространство относительно операции замыкания
представляет собой топологическое пространство относительно операции замыкания  для
для 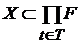 .
. ; аксиома (4):
; аксиома (4):  .
.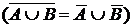 Пусть
Пусть 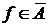 . Тогда каждая окрестность, содержащая
. Тогда каждая окрестность, содержащая 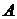 . Значит,
. Значит, 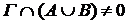 , а отсюда следует, что
, а отсюда следует, что 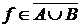 , и тогда
, и тогда 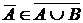 . Аналогично
. Аналогично 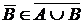 , следовательно,
, следовательно, 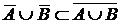 .
.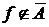 . Тогда
. Тогда 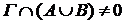 для каждой окрестности Г, содержащей f , и
для каждой окрестности Г, содержащей f , и 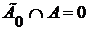 для некоторой окрестности
для некоторой окрестности 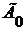 , содержащей f . Если Г – правильная окрестность, содержащая f , то
, содержащей f . Если Г – правильная окрестность, содержащая f , то 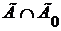 - также окрестность, содержащая f , и поэтому
- также окрестность, содержащая f , и поэтому 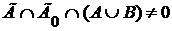 , откуда
, откуда 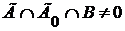 и тем более
и тем более 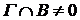 . Это значит, что
. Это значит, что 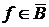 .
.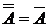 ). Достаточно показать, что
). Достаточно показать, что 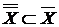 . Пусть
. Пусть 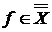 и Г – производная окрестность, содержащая f. Следовательно,
и Г – производная окрестность, содержащая f. Следовательно, 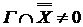 . Возьмем
. Возьмем 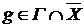 . Тогда Г – окрестность, содержащая g , и т.к.
. Тогда Г – окрестность, содержащая g , и т.к.  , то
, то  . Это значит, что выполняется условие (*) , и поэтому
. Это значит, что выполняется условие (*) , и поэтому 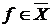 .
.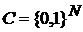 , т.е. декартова степень двухэлементного множества.
, т.е. декартова степень двухэлементного множества.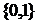 определить топологию, положив
определить топологию, положив 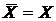 для каждого
для каждого 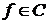 вещественное число
вещественное число 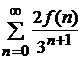 , получаем взаимно однозначное соответствие
, получаем взаимно однозначное соответствие 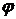 множества
множества 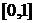 , имеющих в топологическом разложении только цифры 0 и 2.
, имеющих в топологическом разложении только цифры 0 и 2.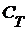 . Это декартова степень
. Это декартова степень 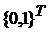 . Топология Тихонова в этом множестве определяется так же, как для множества
. Топология Тихонова в этом множестве определяется так же, как для множества 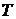 . В действительности можно отождествить множества
. В действительности можно отождествить множества 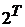 . Поэтому в дальнейшем не будем трактовать множество
. Поэтому в дальнейшем не будем трактовать множество 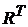 как топологическое пространство. Аналогично можно отождествить элементы множества
как топологическое пространство. Аналогично можно отождествить элементы множества 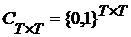 с отношениями над полями, содержащимися в
с отношениями над полями, содержащимися в 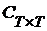 является характеристической функцией множества упорядоченных пар элементов из
является характеристической функцией множества упорядоченных пар элементов из 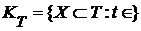 замкнуто и открыто в
замкнуто и открыто в 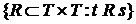 замкнуто и открыто в
замкнуто и открыто в 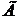 окрестность в
окрестность в 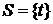 и открытым множеством
и открытым множеством 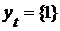 . Тогда
. Тогда 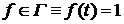 и, значит,
и, значит, 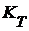 . Таким образом,
. Таким образом, 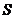 и открытым множеством
и открытым множеством 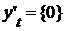 , состоит из характеристических функций множеств, составляющих семейство
, состоит из характеристических функций множеств, составляющих семейство 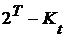 . Эта доказывает, что семейство
. Эта доказывает, что семейство 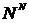 , т.е. множество бесконечных последовательностей натуральных чисел. Топология в
, т.е. множество бесконечных последовательностей натуральных чисел. Топология в 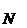 определяется равенством
определяется равенством 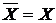 .
. - последовательность из
- последовательность из  членов
членов 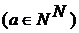 , то множество
, то множество 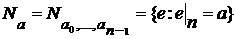 одновременно замкнуто и открыто в
одновременно замкнуто и открыто в 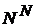 .
. , удовлетворяющих условиям
, удовлетворяющих условиям  для
для 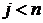 , т.е. оно совпадает окрестностью
, т.е. оно совпадает окрестностью 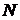 , определенной множеством
, определенной множеством 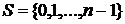 и открытыми множествами
и открытыми множествами 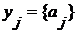 для
для 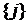 и открытыми множествами
и открытыми множествами 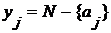 ,
,  число
число 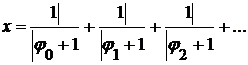 ,
, .
.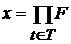 конечно, так и к случаю, когда это множество бесконечно.
конечно, так и к случаю, когда это множество бесконечно.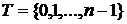 , то декартово произведение
, то декартово произведение 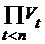 , где для каждого
, где для каждого  множество
множество 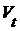 открыто в
открыто в 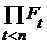 .
.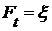 , где
, где  - множество вещественных чисел, то пространство
- множество вещественных чисел, то пространство 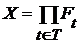 - декартово произведение топологических пространств (с топологией Тихонова),
- декартово произведение топологических пространств (с топологией Тихонова), 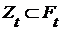 ,
, 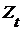 для каждого
для каждого 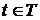 замкнуто в
замкнуто в 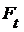 , то
, то 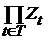 также замкнуто.
также замкнуто.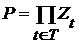 и
и 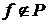 . Тогда
. Тогда 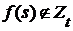 для некоторого
для некоторого 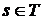 . Окрестность
. Окрестность 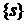 и открытым множеством
и открытым множеством 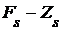 , содержит
, содержит 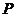 , что и т.д.
, что и т.д. компактно, то пространство
компактно, то пространство 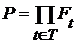 также компактно (в топологии Тихонова).
также компактно (в топологии Тихонова).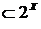 , содержащее R0, т.е. такое, что каждое семейство подмножеств пространства
, содержащее R0, т.е. такое, что каждое семейство подмножеств пространства 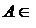 R и
R и 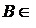 R, то
R, то 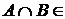 R.
R.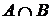 , не было бы центрированным, и, значит, содержало бы конечное подсемейство с пустым пересечением. Очевидно, что множество
, не было бы центрированным, и, значит, содержало бы конечное подсемейство с пустым пересечением. Очевидно, что множество 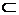 R, что
R, что 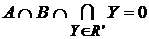 , что противоречит центрированности семейства R.
, что противоречит центрированности семейства R.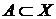 и
и 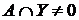 для каждого
для каждого 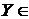 R, то
R, то 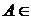 R. В самом деле, в противном случае семейство R
R. В самом деле, в противном случае семейство R  не было бы центрированным и, значит, существовало бы такое конечное подсемейство R'
не было бы центрированным и, значит, существовало бы такое конечное подсемейство R' 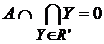 . В силу свойства I произведение
. В силу свойства I произведение 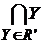 принадлежит R, вопреки тому, что
принадлежит R, вопреки тому, что 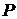 . Обозначим через Rнекоторое центрированное максимальное семейство подмножеств пространства
. Обозначим через Rнекоторое центрированное максимальное семейство подмножеств пространства 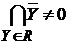 .
.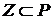 обозначим через
обозначим через 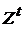 его проекцию на
его проекцию на  R}. Семейство Rt состоит из замкнутых подмножеств пространства
R}. Семейство Rt состоит из замкнутых подмножеств пространства 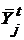 ,
,  R, то
R, то  , т.к. семейство R центрировано. Отсюда следует, что
, т.к. семейство R центрировано. Отсюда следует, что 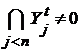 и тем более
и тем более 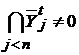 .
.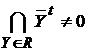 . Использую общий принцип выбора, получаем отсюда, что существует такая функция
. Использую общий принцип выбора, получаем отсюда, что существует такая функция 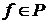 , что
, что 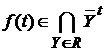 для каждого
для каждого 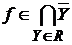 .
. из R и окрестность
из R и окрестность 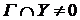 .
.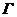 определяется конечным множеством
определяется конечным множеством 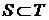 и открытыми множествами
и открытыми множествами 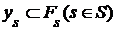 .
.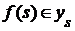 для
для 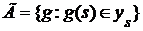 , получим
, получим 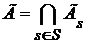 .
.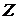 - произвольное множество из R, то
- произвольное множество из R, то 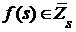 , следовательно,
, следовательно, 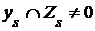 . Поэтому существует такой элемент
. Поэтому существует такой элемент 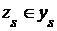 , что
, что 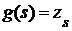 для некоторой функции
для некоторой функции 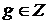 и, значит,
и, значит, 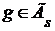 . Таким образом,
. Таким образом, 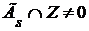 для любого
для любого 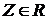 . Отсюда, согласно (II) получаем
. Отсюда, согласно (II) получаем 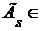 R, а согласно (I),
R, а согласно (I), 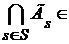 R, т.е.
R, т.е. 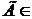 R, откуда
R, откуда 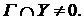 Таким образом, любая окрестность, содержащая
Таким образом, любая окрестность, содержащая 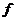 , имеет общие элементы с
, имеет общие элементы с 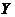 , значит,
, значит, 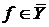 .
. ,
, 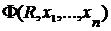 - высказывательная функция, полученная из высказывательных функций
- высказывательная функция, полученная из высказывательных функций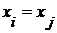
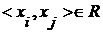 (*)
(*)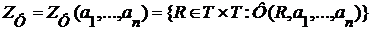 для
для 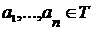 и произвольной открытой высказывательной функции
и произвольной открытой высказывательной функции  .
.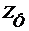 одновременно открыто и замкнуто в
одновременно открыто и замкнуто в 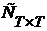 . Действительно, для высказывательных функций (*) это следует из теоремы 2 (§ 6), а для других высказывательных функций – из связи между логическими теоретико-множественными операциями и просто замечания, что сумма, произведение и дополнение открыто-замкнутых множеств тоже открыты и замкнуты.
. Действительно, для высказывательных функций (*) это следует из теоремы 2 (§ 6), а для других высказывательных функций – из связи между логическими теоретико-множественными операциями и просто замечания, что сумма, произведение и дополнение открыто-замкнутых множеств тоже открыты и замкнуты.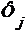 - открытая высказывательная функция с переменными
- открытая высказывательная функция с переменными 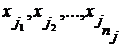 , и пусть
, и пусть  . Из компактности множества
. Из компактности множества 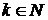 произведение
произведение 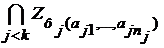 не пусто, то и бесконечное произведение
не пусто, то и бесконечное произведение 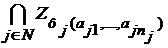 непусто.
непусто.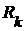 , удовлетворяющих условиям
, удовлетворяющих условиям 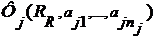 для
для 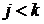
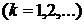 , следует существование одного “универсального” отношения, удовлетворяющего всем этим условиям.
, следует существование одного “универсального” отношения, удовлетворяющего всем этим условиям.