
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расширение упорядоченного множества до полной решетки.
Покажем, что каждое упорядоченное множество О п р е д е л е н и е 1. Реляционная система О п р е д е л е н и е 2. Система В последнем случае говорят также, что система Теорема 1. Каждое упорядоченное множество Д о к а з а т е л ь с т в о. Обозначим Следовательно, функция Расширение, описанное в теореме 1, не сохраняет, вообще говоря, граней, т.е. из равенства Займемся теперь вопросом, можно ли расширить множество Пусть функция О п р е д е л е н и е 3. Погружение  Построим теперь расширение упорядоченного множества до полной решетки с сохранением граней.
Из этих определений непосредственно следует, что
Действительно, по определению Доказательство второго утверждения аналогично.
Включение Второе равенство доказывается аналогично. Введем теперь для упорядоченных множеств понятие сечения. Пара множеств Множество Из этого следует, что В самом деле, каждый элемент множества Наконец, по определению сечения, пара Введем отношение порядка между сечениями: Пусть Обозначим через β - семейство всех сечений. β - полная решетка (8). Пусть
Сечение Если Аналогично доказывается, что сечение (9) Функция Доказательство. Из определений следует, что Из (9) следует Теорема 2. Каждое упорядоченное множество Построенную выше решетку β назовем минимальным расширением упорядоченного множества Займемся более подробно случаем, когда Сначала заметим, что если
Пусть теперь Действительно, Аналогично доказывается, что если Из этих замечаний и равенств (10) получаем, что если
Из определения граней в решетке β (смотреть доказательство утверждения 8) следует, что для любого упорядоченного множества
Наконец, пусть Доказательство (14) самостоятельно. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 250. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
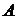 можно рассматривать как часть полной решетки (а именно такой, в которой выполняются основные законы алгебры множеств). Рассмотрим аналогичную проблемы для булевых колец. Для этого введем сначала общее понятие вложения одной реляционной системы в другую.
можно рассматривать как часть полной решетки (а именно такой, в которой выполняются основные законы алгебры множеств). Рассмотрим аналогичную проблемы для булевых колец. Для этого введем сначала общее понятие вложения одной реляционной системы в другую. называется подсистемой системы
называется подсистемой системы  , если
, если 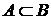 и
и 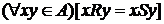 (т.е.
(т.е.  ).
).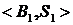 системы
системы  можно погрузить в семейство всех подмножеств некоторого множества (упорядоченное отношение включения) и, значит, в некоторое полное атомарное булево кольцо.
можно погрузить в семейство всех подмножеств некоторого множества (упорядоченное отношение включения) и, значит, в некоторое полное атомарное булево кольцо. . Из транзитивности отношения
. Из транзитивности отношения  следует, что
следует, что  . Т.к.
. Т.к. 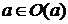 , то
, то  . Таким образом,
. Таким образом,  , откуда
, откуда 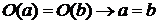 .
. погружает
погружает  , упорядоченное отношением
, упорядоченное отношением 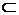 . Это семейство, очевидно, можно расширить до семейства
. Это семейство, очевидно, можно расширить до семейства 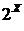 , где
, где  .
. (или
(или  ) не следует
) не следует  (или
(или  ).
).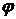 погружает упорядоченную систему
погружает упорядоченную систему  в упорядоченную систему
в упорядоченную систему  .
.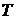 и каждой функции
и каждой функции  , для которой существует
, для которой существует 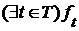 , существует также
, существует также  и
и 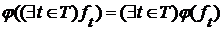 . Аналогично для нижних граней.
. Аналогично для нижних граней. Пусть
Пусть 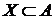 положим
положим ,
, .
.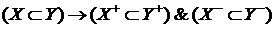 (1),
(1), и
и  для любого
для любого 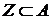 (2).
(2). , поэтому
, поэтому  .
. (3)
(3) следует из (2). Пусть
следует из (2). Пусть  . Тогда
. Тогда  и тем более
и тем более  , поскольку
, поскольку 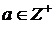 .
. называется сечением упорядоченного множества
называется сечением упорядоченного множества  и
и 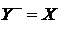 .
. называется нижним классом, а
называется нижним классом, а 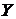 - верхним классом сечения.
- верхним классом сечения. (4).
(4). находится в отношении
находится в отношении  к каждому элементу множества
к каждому элементу множества 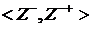 и каждая пара вида
и каждая пара вида  являются сечениями. Любое сечение можно представить в любом из этих видов.
являются сечениями. Любое сечение можно представить в любом из этих видов. , где
, где 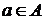 является сечением (6).
является сечением (6).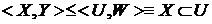 . Для проверки того, что отношение
. Для проверки того, что отношение  (7).
(7). и
и  . Если
. Если  , то
, то 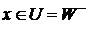 , а поэтому
, а поэтому 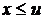 . Отсюда
. Отсюда  и, значит,
и, значит, 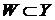 . Аналогично доказывается обратная к (7) импликация.
. Аналогично доказывается обратная к (7) импликация. . Обозначим :
. Обозначим :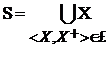 ,
,  .
. является наименьшей верхней гранью множества £. Действительно,
является наименьшей верхней гранью множества £. Действительно, 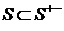 , следовательно,
, следовательно,  для каждого
для каждого 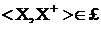 .
. для каждого
для каждого  , то
, то 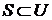 . Отсюда
. Отсюда  , и тогда
, и тогда  .
.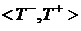 является наибольшей нижней гранью множества £.
является наибольшей нижней гранью множества £. погружает
погружает  . Возьмем
. Возьмем  в множестве
в множестве  , а поэтому
, а поэтому  для
для 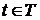 . Пусть сечение
. Пусть сечение  для
для  , а т.к.
, а т.к.  , то
, то  . Значит,
. Значит,  для любого
для любого  , откуда следует, что
, откуда следует, что  . Поэтому
. Поэтому  , откуда
, откуда  и
и  . Таким образом,
. Таким образом,  в множестве β. Для нижней грани доказательство аналогично.
в множестве β. Для нижней грани доказательство аналогично. и
и  - произвольные подмножества упорядоченного множества
- произвольные подмножества упорядоченного множества 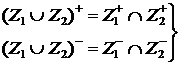 (10)
(10) и
и 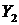 - верхние классы двух сечений в
- верхние классы двух сечений в  - множество всех элементов вида
- множество всех элементов вида 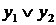 , где
, где  для
для  .
. и, значит,
и, значит,  для
для 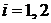 . Кроме того,
. Кроме того, 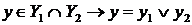 .
. и
и  - нижние классы двух сечений в
- нижние классы двух сечений в  - множество всех элементов вида
- множество всех элементов вида  , где
, где  для
для  - два ее сечения, то
- два ее сечения, то ,
, (11).
(11). (12),
(12), (13).
(13). для произвольного множества
для произвольного множества 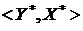 - также сечение в
- также сечение в