
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приведенные Декартовы произведения.
Комбинируя операцию образования декартова произведения с операцией образования классов абстракций, получаем новую операцию, которая нашла применение в матлогике. Пусть Пусть
Tеорема 1. Отношение 1) Рефлексивность отношения
Теорема 2. Декартово произведение Д о к а з а т е л ь с т в о. Необходимо показать, что если Пусть Поэтому Из теорем 1, 2 и следствий, приведенных в § 5 главе III, вытекает, что существует множество Множество Пусть  Зная множества Для решения этой проблемы рассмотрим более общую высказывательную функцию Докажем, что справедливы утверждения (I) – (IV). I. Действительно, II. Если В самом деле, пусть Для Обозначим множество этих элементов Тогда
откуда Обратно, если Идеал Пример простого идеала дает семейство (III). Если идеал Действительно, (IV). Если идеал Доказанные утверждения дают следующее решение поставленной выше проблемы. Назовем высказывательную функцию a) b) c) С помощью операций исчисления высказываний и кванторов °Теорема 3. Если Д о к а з а т е л ь с т в о. Если в случае a) левая часть (2) эквивалентна в случае b) левая часть (2) эквивалентна в случае c) левая часть (2) эквивалентна Правая часть (2) эквивалентна
из определения множеств В силу утверждений (I)-(IV), если формула (2) справедлива для высказывательных функций °Следствие 4. Если высказывательная функция °Следствие 5. Если Это легко получается из предыдущего следствия с учетом того, что если Рассмотрит примеры, считая Пример 1. Если отношения
Пример 2. Если Аналогично, если каждое из множеств Эти утверждения получаются из следствия 5, если высказывательные функции « Эти примеры показывают, что операция образования приведенного декартова позволяет получить из данного семейства моделей для произвольной системы аксиом (которые можно выразить с помощью элементарных высказывательных функций) новые модели для этой же системы. Другие применения приведенных декартовых произведений будут даны в главе IX.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 265. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
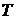 - произвольное множество и
- произвольное множество и 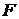 - функция, определенная на
- функция, определенная на  определена функция
определена функция  со значениями в
со значениями в 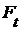 и что
и что  - бинарное отношение над полем, содержащемся в
- бинарное отношение над полем, содержащемся в 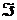 - идеал в
- идеал в  . Определим отношение
. Определим отношение  в
в  формулой
формулой
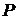 .
. , 2) симметричность очевидна, a 3) транзитивность следует из того, что произвольных
, 2) симметричность очевидна, a 3) транзитивность следует из того, что произвольных 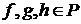
 .
.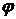 функции
функции  , то
, то  .
.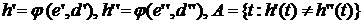 . Из определения
. Из определения  следует, что
следует, что  .
.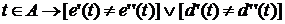 , откуда
, откуда 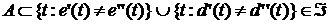 .
. классов абстракций отношения
классов абстракций отношения  , индуцированная из
, индуцированная из  в
в  , где
, где 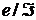 ,
,  - классы абстракций , содержащие соответственно
- классы абстракций , содержащие соответственно 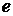 и
и 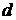 .
. - произвольная высказывательная функция. Главную проблему в теории приведенных произведений можно сформулировать так:
- произвольная высказывательная функция. Главную проблему в теории приведенных произведений можно сформулировать так: , определить, когда множество
, определить, когда множество  .
. произвольного числа переменных. Пусть
произвольного числа переменных. Пусть 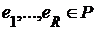 и
и  . (Очевидно, что множество
. (Очевидно, что множество  зависит не только от
зависит не только от  , но мы это не отмечаем в индексе при
, но мы это не отмечаем в индексе при  .
.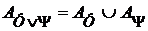 и поэтому ((II), §5, глава I)
и поэтому ((II), §5, глава I)  , откуда по закону де Моргана получим (I).
, откуда по закону де Моргана получим (I).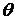 - высказывательная функция вида (
- высказывательная функция вида (  )
) 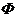 , то
, то  .
. .
. существует элемент
существует элемент  , удовлетворяющий
, удовлетворяющий  .
.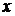 через
через  и положим
и положим  для
для  . Пусть
. Пусть 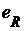 - функция выбора для семейства, состоящего из всех множеств
- функция выбора для семейства, состоящего из всех множеств  и для всех
и для всех  . Следовательно,
. Следовательно,  .
.
 , откуда
, откуда  и
и  .
. либо
либо  , либо
, либо 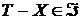 .
.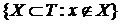 . В главе VII (пользуясь аксиомой выбора) мы докажем, что любой идеал можно расширить до простого.
. В главе VII (пользуясь аксиомой выбора) мы докажем, что любой идеал можно расширить до простого.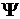 - отрицание
- отрицание  , то
, то  .
. .
. если, кроме того,
если, кроме того,  обозначит
обозначит  , то
, то  . Это утверждение следует из первых трех.
. Это утверждение следует из первых трех. элементарной, если она получается из высказывательных функций :
элементарной, если она получается из высказывательных функций :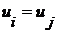


 .
. - элементарная высказывательная функция,
- элементарная высказывательная функция,  - произвольные элементы из
- произвольные элементы из 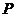 , то
, то  (2).
(2).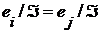 ,
, ,
, .
. в случае a)
в случае a)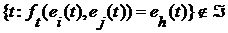 в случае b)
в случае b)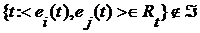 в случае c)
в случае c) . Это следует из теоремы 3 , если высказывательная функция не содержит переменных
. Это следует из теоремы 3 , если высказывательная функция не содержит переменных  .
. для каждого
для каждого  .
. .
. .
. ,
, 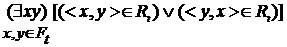 , то отношение
, то отношение  , то множества
, то множества  , где
, где 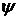 - декартовы произведения
- декартовы произведения  - тело с операциями
- тело с операциями  и
и 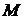 » и «
» и «  » записать в виде элементарных высказывательных функций
» записать в виде элементарных высказывательных функций  и
и  соответственно.
соответственно.