
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Бесконечные операции в решетках и булевых кольцах.
Утверждения, доказанные в предыдущих параграфах этой главы, можно рассматривать как термины о решетке Предположим сначала, что Теорема 1. Наименьшая верхняя грань
(соответственно Теорема 2. Если Теорема 3. Если Для произвольного упорядоченного множества можно доказать утверждение, аналогичное (3), § 1. Теорема 4. Если существуют грани Формулы (4)-(11) § 1 не имеют аналогов в произвольных упорядоченных множествах. Теорема 5. Если Д о к а з а т е л ь с т в о. В самом деле, Условие, что  Теорема 6. Если |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 265. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
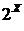 . Как мы знаем, эта решетка полна и является булевой алгеброй. Естественно возникает вопрос, можно ли обобщить термин №1 на произвольные решетки, полные решетки, булевы кольца.
. Как мы знаем, эта решетка полна и является булевой алгеброй. Естественно возникает вопрос, можно ли обобщить термин №1 на произвольные решетки, полные решетки, булевы кольца.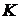 - произвольное упорядоченное множество и
- произвольное упорядоченное множество и 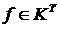 . Тогда справедливы теоремы, аналогичные теоремам 1-3 §1.
. Тогда справедливы теоремы, аналогичные теоремам 1-3 §1.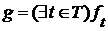 (наименьшая нижняя грань
(наименьшая нижняя грань  ), если она существует, является единственным элементом множества
), если она существует, является единственным элементом множества  , удовлетворяющим условиям:
, удовлетворяющим условиям:
 ).
).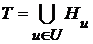 и для каждого
и для каждого 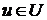 существует наименьшая верхняя грань
существует наименьшая верхняя грань  , и если существует наименьшая верхняя грань
, и если существует наименьшая верхняя грань  . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней.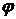 - перестановка множества
- перестановка множества 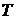 и существует наименьшая верхняя грань
и существует наименьшая верхняя грань  . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней.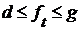 для всех
для всех 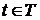 .
.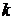 - решетка,
- решетка,  и существуют наименьшие верхние грани
и существуют наименьшие верхние грани  ,
, 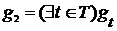 , то существует наименьшая верхняя грань
, то существует наименьшая верхняя грань  и она равна
и она равна  . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней. для любого
для любого 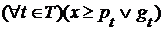 , то
, то 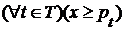 . Поэтому
. Поэтому  и аналогично
и аналогично  , откуда
, откуда  .
. и
и 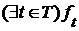 и
и 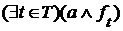 , то
, то  .
.