
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обобщённые декартовы произведения.Пусть О п р е д е л е н и е. Декартовым произведением
Если Если все сомножители Для Замечание. Пусть В самом деле, если Теорема 1. Если Д о к а з а т е л ь с т в о. Проведем индукцию по числу элементов множества Пусть Теорема 1 распространяется также на случай произвольного Теорема 2. Если В общем случае доказательство того, что декартово произведение непустых множеств непусто, требует аксиомы выбора.  ºTеорема 3. Если Д о к а з а т е л ь с т в о. Элементами множества Пользуясь декартовыми произведениями (например в алгебре, топологии и т.п.), мы обычно сталкиваемся со случаями, когда на множествах Другими словами, кроме функции Функция
Таким образом, Аналогично определяется декартово произведение отношений. Пусть Декартовым произведением отношения называется такое отношение Здесь надо заметить, что Очевидно, что все эти определения без труда переносятся на случай, когда на каждом множестве Пример. Предположим, что Теорема 4. Декартово произведение Д о к а з а т е л ь с т в о. Достаточно проверить справедливость аксиомы булевой алгебры (I – V', §9, гл. I). Проверим, например, справедливость (IV). Пусть Булево кольцо Аналогично определяется прямое произведение группы колец и других алгебраических систем.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 263. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
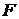 (как в §1) – функция, значениями которой являются подмножества множества
(как в §1) – функция, значениями которой являются подмножества множества  , а областью определения – множество
, а областью определения – множество  .
. называется множество таких функций
называется множество таких функций  с областью определения
с областью определения 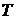 , что
, что  для каждого
для каждого  :
: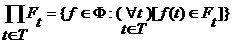 , где
, где  .
. , то вместо
, то вместо  пишут
пишут  . Элементами этого декартова произведения будут такие последовательности
. Элементами этого декартова произведения будут такие последовательности 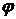 , что
, что  для
для 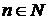 .
. равны,
равны,  , то
, то 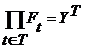 . Здесь
. Здесь 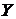 . Множество
. Множество  называется декартовой степенью множества
называется декартовой степенью множества  обозначим через
обозначим через 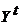 проекцию множества
проекцию множества  , т.е.
, т.е.  . Очевидно, что
. Очевидно, что 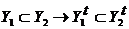 для каждого
для каждого  . Декартовы произведения
. Декартовы произведения  не совпадают. Первое имеет в качестве элементов последовательности длины 2, второе – упорядоченные пары, а это различные понятия. Однако в действительности различие между этими двумя произведениями не существенно, потому что каждой упорядоченной паре
не совпадают. Первое имеет в качестве элементов последовательности длины 2, второе – упорядоченные пары, а это различные понятия. Однако в действительности различие между этими двумя произведениями не существенно, потому что каждой упорядоченной паре 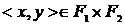 можно поставить во взаимно однозначное соответствие последовательность
можно поставить во взаимно однозначное соответствие последовательность  . Если
. Если  для некоторого
для некоторого  , то
, то  .
. , то
, то 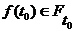 , т.е.
, т.е.  .
. для каждого
для каждого  .
.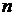 элементов. Пусть
элементов. Пусть  , где
, где  .
. . Докажем, что
. Докажем, что  . Тогда множество
. Тогда множество  будет функцией, принадлежащей
будет функцией, принадлежащей  , следовательно, множество
, следовательно, множество  , то
, то  .
. .
. , задана
, задана  такая функция
такая функция  двух переменных, что
двух переменных, что 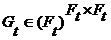 для каждого
для каждого 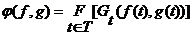 , где
, где  .
. - такой элемент
- такой элемент  декартова произведения, что
декартова произведения, что  для всех
для всех  . Операция
. Операция  .
. - такая функция, что
- такая функция, что 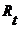 (для каждого
(для каждого  .
. - множество функций. Однако можно естественным образом поставить в соответствие декартову произведению
- множество функций. Однако можно естественным образом поставить в соответствие декартову произведению  , которое выполняется тогда и только тогда, когда функция
, которое выполняется тогда и только тогда, когда функция 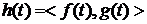 (т.е. функция
(т.е. функция  ), принадлежит
), принадлежит  - булево кольцо относительно операций
- булево кольцо относительно операций 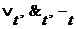 и элементов
и элементов  . Обозначим через
. Обозначим через  декартовы произведения операций
декартовы произведения операций 
 и
и  такие функции, что
такие функции, что  и
и  для всех
для всех  - это такая функция
- это такая функция 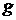 , что
, что  для каждого
для каждого  и, значит,
и, значит,  .
.