
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теория представления дистрибутивных решеток.
Основное понятие в этой теории – понятии идеала. Определение. Идеалом дистрибутивной решетки
За последнее время многие авторы вместо идеала используют понятие фильтра, т.е. подмножества множества
Все приведенные ниже теоремы об идеалах можно превратить в теоремы о фильтрах простой заменой символов Понятие фильтра двойственно к понятию идеала, поэтому достаточно рассматривать какое-либо одно из них (смотреть Р. Сикорский «Булевы алгебры», страница 25). Идеал
Пример 1. Пусть А - решетка множеств (например, всех подмножеств произвольного множества Если Пример 2. Семейство всех конечных множеств Пример 3. Если А - семейство всех подмножеств множества вещественных чисел, то семейство множеств Лебедевой меры В произвольной решетке множество Мы будем пользоваться следующими общими свойствами идеалов:
Действительно, Если
Действительно, (6) Множество  В самом деле, если (7) Пусть идеалы Действительно, если Если Если Действительно, таким идеалом будет множество Пусть Если решетка В самом деле, возьмем ( Элементы Таким образом, предположение, что ни В главе (VII) из (7) и (8) мы получили (с помощью аксиомы выбора) следующий результат: семейство Итак, мы ввели понятия дистрибутивной решетки, булева кольца, решетки множеств, тела множеств. Привели схему, показывающую взаимосвязь между этими понятиями:
Докажем, что каждая дистрибутивная решетка изоморфна решетке множеств, а каждое булево кольцо с 1 – телу множеств. °Tеорема 1. Для каждой дистрибутивной решетки существует изоморфная ей решетка множеств. Д о к а з а т е л ь с т в о. Пусть Это соответствие взаимно однозначно. Действительно, если В первом случае Из (1) и (4) получаем
Эти равенства доказывают, что класс, составленный из всех семейств °Теорема 2. Для каждого булево кольца существует изоморфное тело множеств. Д о к а з а т е л ь с т в о. Если решетка Приведем для теоремы 2 еще топологическую интерпретацию. Пусть Для любого множества °Теорема 3. I. II. Множества III. Каждое открытое и замкнутое множество в Д о к а з а т е л ь с т в о. Проверку аксиом топологии выполнить самостоятельно. Для того, чтобы доказать, что пространство Покажем, что Обозначим через Очевидно, что Покажем, что
Таким образом, в силу (10) существует простой идеал Пусть II-е утверждение справедливо, поскольку семейство Чтобы доказать III-е утверждение, предположим, что множество Построенное в теореме 3 пространство Из теоремы 3 вытекает °Следствие 4. Каждое булево кольцо с единицей изоморфно телу открыто-замкнутых множеств компактного пространства.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 321. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называется такое непустое множество
называется такое непустое множество  , что
, что (1),
(1),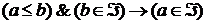 (2) (смотреть (II) §5, глава I )
(2) (смотреть (II) §5, глава I )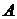 , удовлетворяющего условиям, двойственным условиям (1), (2):
, удовлетворяющего условиям, двойственным условиям (1), (2): (1'),
(1'), (2').
(2'). на &,
на &,  на
на  .
.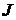 называется простым, если
называется простым, если  и для
и для 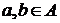 :
: (3).
(3). ) и
) и 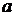 - произвольный элемент суммы S(А). Семейство
- произвольный элемент суммы S(А). Семейство 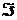 множеств
множеств  А, не содержащих элемент
А, не содержащих элемент 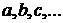 - произвольные, не совпадающие элементы суммы S(А), то семейство тех
- произвольные, не совпадающие элементы суммы S(А), то семейство тех  образует идеал вА.
образует идеал вА. есть идеал, который называется главным идеалом, порожденным элементом
есть идеал, который называется главным идеалом, порожденным элементом  (4).
(4).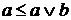 ,
,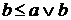 .
. , то
, то  и
и  , в силу (2)
, в силу (2)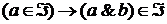 (5).
(5). .
. таких элементов
таких элементов 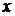 , что
, что  для некоторого
для некоторого  , является идеалом и
, является идеалом и 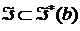 ,
,  .
. и
и 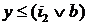 , то
, то  , откуда
, откуда  , поскольку
, поскольку  . Если
. Если 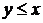 , то
, то 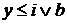 . Таким образом,
. Таким образом,  для
для 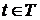 образуют такое монотонное семейство идеалов, что
образуют такое монотонное семейство идеалов, что  ,
,  для каждого
для каждого  . Тогда сумма
. Тогда сумма  является идеалом и
является идеалом и  . (лекция “Топология I”, страница 33).
. (лекция “Топология I”, страница 33).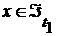 и
и  , то оба элемента
, то оба элемента  принадлежат либо
принадлежат либо  , либо
, либо 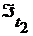 . В каждом из этих случаев
. В каждом из этих случаев 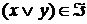 .
. и
и  , то
, то  , а поэтому
, а поэтому 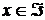 . Таким образом,
. Таким образом,  , то существует такой идеал
, то существует такой идеал  - отрицание.
- отрицание. 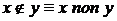 ,
,  ) (8).
) (8).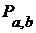 - семейство всех идеалов, содержащих
- семейство всех идеалов, содержащих  .
. . Если
. Если  , то
, то  , а тогда
, а тогда  , то и
, то и  , откуда
, откуда  для некоторого
для некоторого 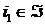 . Аналогично, если
. Аналогично, если  , то
, то  для некоторого
для некоторого 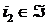 . В силу дистрибутивности решетки
. В силу дистрибутивности решетки  I)
I) 
 ,
, 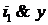 и
и  принадлежат
принадлежат  мы взяли из
мы взяли из  .
. не принадлежит
не принадлежит  имеет максимальный элемент, т.е. существует идеал
имеет максимальный элемент, т.е. существует идеал 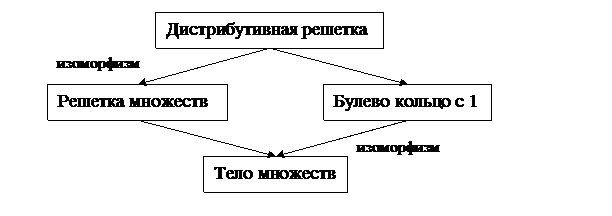

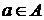 ставим в соответствие семейство
ставим в соответствие семейство  простых идеалов, для которых
простых идеалов, для которых  .
.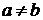 , то либо
, то либо 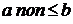 , либо
, либо  , т.е. такой, что либо
, т.е. такой, что либо  ,
,  , во втором случае
, во втором случае  ,
,  . В обоих случаях
. В обоих случаях  .
. а из (3) и (5)
а из (3) и (5) Следовательно,
Следовательно,  ,
,  .
.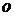 , единичный
, единичный  , и для каждого
, и для каждого  , что
, что  и
и 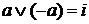 . При соответствии
. При соответствии  элементу о соответствует пустое множество, а элементу
элементу о соответствует пустое множество, а элементу  и
и  , то
, то 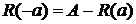 . Таким образом, множество всех семейство
. Таким образом, множество всех семейство 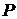 - множество всех простых идеалов кольца
- множество всех простых идеалов кольца 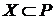 будем считать, что
будем считать, что  , если каждая окрестность идеала
, если каждая окрестность идеала 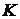 замкнутых множеств.
замкнутых множеств. .
. семейство всех конечных произведений вида
семейство всех конечных произведений вида  , где
, где  - произвольное натуральное число, и
- произвольное натуральное число, и  . Таким образом, семейство
. Таким образом, семейство  .
. . Если
. Если  , то
, то  для некоторых
для некоторых 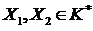 , поэтому
, поэтому 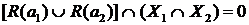 . Т.к.
. Т.к.  и
и 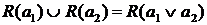 , то
, то  . Следовательно,
. Следовательно,  . В противном случае для некоторого множества
. В противном случае для некоторого множества  было бы
было бы , откуда
, откуда  , т.е.
, т.е.  , вопреки центрированности семейства
, вопреки центрированности семейства  . Значит, он принадлежит
. Значит, он принадлежит 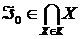 .
. и тем более
и тем более  для каждого
для каждого  ; в частности,
; в частности,  . Следовательно, каждая окрестность идеала
. Следовательно, каждая окрестность идеала  , откуда
, откуда  I. Теорема 3 доказано.
I. Теорема 3 доказано. открыто, т.к. оно равно
открыто, т.к. оно равно  , т.е. также окрестность.
, т.е. также окрестность.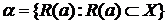 . Т.к. каждый элемент открытого множества
. Т.к. каждый элемент открытого множества  и поэтому
и поэтому  . Следовательно, семейство, составленное из множества
. Следовательно, семейство, составленное из множества  , где
, где 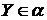 , имеет пустое пересечение. Поскольку оно состоит из всех замкнутых множеств, оно не центрировано, т.е. существует такое конечное подмножество
, имеет пустое пересечение. Поскольку оно состоит из всех замкнутых множеств, оно не центрировано, т.е. существует такое конечное подмножество  семейства
семейства  , что
, что  . Тогда
. Тогда 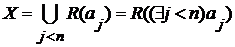 , т.е.
, т.е.