
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обратные системы и их пределы.
Пусть даны: a) произвольное множество b) упорядоченно (или квазиупорядоченное) отношение c) функция d) функция Пусть функция
Система
Пусть
тогда
Если даны две обратные системы :
Коммутативна, т.е.
Была коммутативна для каждого Для этого достаточно для каждого Легко доказать, что если Пример 1. Пусть множество Пример 2. Пусть множество  Для доказательства заметим, что если Отсюда Пример 3. Множество Здесь роль множества Поставим в соответствие каждому элементу Легко проверить, что При этом Наконец, отображение Следует отметить, что все эти рассуждения остаются в силе, если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, множество
множество 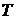 ,
, , такая, что
, такая, что  для каждого
для каждого 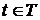 ,
, , которую можно записать в виде
, которую можно записать в виде  или
или 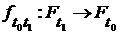 , где
, где  (1)
(1) удовлетворяет условиям
удовлетворяет условиям  (2),
(2), для каждого
для каждого  называется обратной системой. Обратным пределом этой системы, обозначенным
называется обратной системой. Обратным пределом этой системы, обозначенным  или
или  , называется подмножество произведения
, называется подмножество произведения 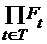 , состоящее из таких элементов
, состоящее из таких элементов 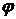 , что
, что (4).
(4). обозначает
обозначает  -ю координатную функцию
-ю координатную функцию  , определенную равенством
, определенную равенством (5)
(5) (6)
(6) и
и  и функция
и функция  , т.е.
, т.е.  , и диаграмма
, и диаграмма 

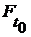

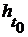




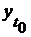



 , если
, если  , чтобы диаграмма
, чтобы диаграмма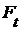




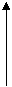



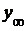

 задать
задать  условием
условием  .
. .
.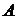 , упорядоченное (или квазиупорядоченное) отношением
, упорядоченное (или квазиупорядоченное) отношением  , существует такое
, существует такое  , что
, что  и
и  .),
.),  для каждого
для каждого  - тождественное отображение. Тогда
- тождественное отображение. Тогда 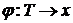 .
. , то существует такое
, то существует такое  , что
, что  и
и  .
. , и тогда, согласно (4),
, и тогда, согласно (4),  . Аналогично
. Аналогично  , поэтому
, поэтому  .
.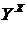 всех отображений
всех отображений  можно с помощью операции сужения
можно с помощью операции сужения  представить как обратный предел множества
представить как обратный предел множества  , где
, где  . Для этого надо в качестве направленного множества
. Для этого надо в качестве направленного множества 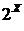 , упорядоченное отношением включения, функцию
, упорядоченное отношением включения, функцию 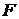 задать равенством
задать равенством  для
для  поставить в соответствие функцию
поставить в соответствие функцию  , определенную равенством
, определенную равенством  , где
, где  .
.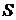 всех сужений, т.е.
всех сужений, т.е.  .
.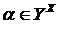 элемент
элемент  , определенный условием
, определенный условием 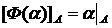 .
. , т.е.
, т.е.  .
. отображает
отображает 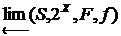 . Действительно, пусть
. Действительно, пусть  , тогда
, тогда  для каждого
для каждого 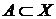 . Определим
. Определим 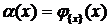 . Легко видеть, что
. Легко видеть, что  , т.е.
, т.е.  для
для 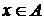 .
. , то существует такое
, то существует такое  ,
,  , т.е.
, т.е. 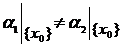 . Следовательно,
. Следовательно,  , так что
, так что  .
. - метрические пространства. Тогда
- метрические пространства. Тогда  .
.