
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 3. Семейство содержит в качестве подмножеств каждое из семейств
Вообще говоря, никакие два из этих семейств не совпадают; кроме того, они не исчерпывают всего семейства Опишем теперь метод, позволяющий решить, принадлежит ли данное множество, определенное при помощи высказывательной функции, семейству Пусть Теорема 4. Если для произвольных Д о к а з а т е л ь с т в о. Проведем индукцию по числу кванторов. 1) Если 2) Если теорема верна для
Наиболее интересный пример семейства Пример. Докажем, что множество предельных точек последовательности непрерывных функций есть множество типа Для этого запишем условие Коши сходимости последовательности вещественных чисел
Отсюда видно, что множество
Полагая
получаем
Т.к.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 272. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
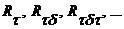

 .
. - высказывательная функция, переменные
- высказывательная функция, переменные  пробегают множество
пробегают множество 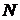 . Положим
. Положим  ,
,  , где каждый из символов
, где каждый из символов  обозначает либо квантор всеобщности, либо квантор существования.
обозначает либо квантор всеобщности, либо квантор существования. множество
множество  принадлежит
принадлежит 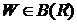 .
. , то
, то  и тогда
и тогда  по условию.
по условию. квантора, то каждое из множеств
квантора, то каждое из множеств  принадлежит
принадлежит  - квантор существования, то
- квантор существования, то 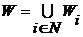 , а если
, а если  . В обоих случаях
. В обоих случаях  возьмём семейство
возьмём семейство 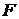 замкнутых множеств произвольного топологического пространства
замкнутых множеств произвольного топологического пространства  . В этому случае
. В этому случае  .
. ,
,  , …,
, …,  ,…:
,…:
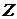 предельных точек последовательности непрерывных функций
предельных точек последовательности непрерывных функций 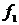 ,
,  , ..., fn, …, имеет вид:
, ..., fn, …, имеет вид:
 ,
,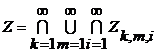 .
. (при фиксированных индексах) замкнуто (это следует из непрерывности рассматриваемых функций), то
(при фиксированных индексах) замкнуто (это следует из непрерывности рассматриваемых функций), то