Семейства множеств, замкнутые относительно данной операции.
Пусть  - некоторое фиксированное множество, - некоторое фиксированное множество,  - функция произвольного числа переменных, каждое из которых пробегает какое-нибудь семейство подмножеств множества - функция произвольного числа переменных, каждое из которых пробегает какое-нибудь семейство подмножеств множества  . .
Для простоты изложения будем считать, что  - функция 2-х переменных, т.е. областью её определения является декартово произведение - функция 2-х переменных, т.е. областью её определения является декартово произведение  . Семейство . Семейство  называется замкнутыми относительно называется замкнутыми относительно  , если , если
 . .
Теорема 1. Для каждого семейства  существует такое семейство существует такое семейство  , что , что
a)  , ,
b) Семейство  замкнуто относительно операции замкнуто относительно операции  , ,
c) Семейство  - наименьшее из семейств, обладающих свойствами a) и b), т.е. если для - наименьшее из семейств, обладающих свойствами a) и b), т.е. если для  выполнены условия выполнены условия
 , , 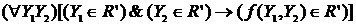 , (1) , (1)
то 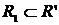 . .
Д о к а з а т е л ь с т в о. Пусть 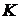 - множество всех семейств - множество всех семейств  , для которых выполняется (1). , для которых выполняется (1).  , т.к. , т.к.  . Искомым семейством . Искомым семейством  будет произведение будет произведение  . .
Семейство  , обладающее свойствами a) – c), определяется однозначно. Действительно, если , обладающее свойствами a) – c), определяется однозначно. Действительно, если 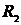 обладает этими свойствами, то из минимальности семейства обладает этими свойствами, то из минимальности семейства  (свойство c)) получает (свойство c)) получает  . Аналогично, . Аналогично, 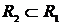 , т.к. , т.к. 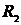 также обладает свойством c). Следовательно, также обладает свойством c). Следовательно,  , мы будет обозначать это , мы будет обозначать это  семейство семейство 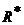 . .
Теорема 2. Для произвольных семейств  , ,  , , 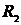 выполняются следующие условия: выполняются следующие условия:
I. 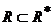 , ,
II.  , ,
III.  . .
Д о к а з а т е л ь с т в о. I) Следует из теоремы 1 (свойство a)). II) следует из того, что  замкнуто относительно замкнуто относительно  и содержит и содержит  , значит, в силу минимальности , значит, в силу минимальности  . Для доказательства III заметим, что из условия I следует . Для доказательства III заметим, что из условия I следует 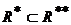 , с другой стороны, , с другой стороны, 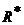 замкнуто относительно замкнуто относительно  , поэтому , поэтому 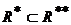 . .
 . .
Теорема 1 и теорема 2 имеют свои аналоги для случая, когда дана не одна функция  , а произвольное семейство таких функция, и , а произвольное семейство таких функция, и 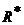 - наименьшее семейство, содержащее - наименьшее семейство, содержащее  и замкнутое относительно всех функций. Областями определения этих функций могут быть последовательности подмножеств или даже семейства подмножеств множества и замкнутое относительно всех функций. Областями определения этих функций могут быть последовательности подмножеств или даже семейства подмножеств множества  . Мы не будет останавливаться на этих обобщениях. . Мы не будет останавливаться на этих обобщениях.
Пример 1. Пусть  - обозначает сложение множеств, т.е. - обозначает сложение множеств, т.е.  . Наименьшее семейство множеств, содержащее . Наименьшее семейство множеств, содержащее  и замкнутое относительно и замкнутое относительно  , обозначим символом , обозначим символом 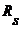 . Это семейство состоит из конечных сумм вида . Это семейство состоит из конечных сумм вида  , где , где  , ,  и и  - последовательность множеств, принадлежащих - последовательность множеств, принадлежащих  , т.е. , т.е.  . .
Аналогично, если функция 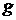 задаётся равенством задаётся равенством  , то наименьшее семейство, содержащее , то наименьшее семейство, содержащее  и замкнутое относительно и замкнутое относительно 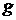 , обозначим символом , обозначим символом  . Это семейство состоит из произведений вида . Это семейство состоит из произведений вида  , где , где  , ,  , ,  . .
Пример 2. Решеткой множеств, порождённой семейством  , назовем наименьшее семейство, содержащее , назовем наименьшее семейство, содержащее  и замкнутое относительно обеих операций и замкнутое относительно обеих операций  , , 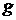 из примера 1. из примера 1.
Теорема 3. Решетка множества, порождённая  , совпадает с семейством , совпадает с семейством 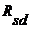 , причем , причем  . .
Д о к а з а т е л ь с т в о. Докажем вначале вторую часть теорема, т.е.  . .
Пусть 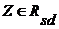 , т.е. , т.е.  , где , где  , ,  и и 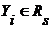 для для  . .
Докажем индукцией по 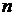 , что , что 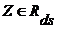 . Для . Для 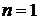 имеем имеем 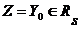 , а , а 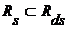 , т.к. , т.к. 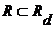 . Предположим, что теорема верна для . Предположим, что теорема верна для 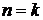 . .
Пусть 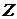 - произведение - произведение 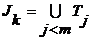 , где , где  , ,  и и  для для  . Обозначим . Обозначим  . По предположению индукции . По предположению индукции  и, значит, и, значит, 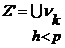 , где , где  , ,  и и 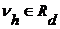 для для  . .
Т.к. 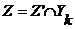 , то , то  . .
Поскольку 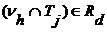 , получаем отсюда, что , получаем отсюда, что 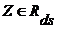 . Таким образом, . Таким образом,  . Аналогично доказывается обратное включение. . Аналогично доказывается обратное включение.
Теперь докажем, что 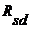 - решетка множеств, порожденная множеством - решетка множеств, порожденная множеством  . Ясно, что семейство . Ясно, что семейство 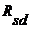 содержится в этой решетке, т.к. операции сложения и умножения не выводят нас из решетки. С другой стороны, содержится в этой решетке, т.к. операции сложения и умножения не выводят нас из решетки. С другой стороны,
 , ,
следовательно, семейство 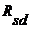 замкнуто относительно операций сложения и умножения и потом содержит решетку, порождённую замкнуто относительно операций сложения и умножения и потом содержит решетку, порождённую  . .
§4. 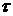 - аддитивные и - аддитивные и 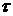 - мультипликативные семейства множеств. - мультипликативные семейства множеств.
Семейство множеств  называется называется 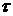 - аддитивным (соответственно - аддитивным (соответственно 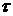 - мультипликативным), если - мультипликативным), если  (соответственно (соответственно 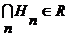 ) для каждой последовательности ) для каждой последовательности 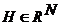 . .
Из теоремы 1, теоремы 2 (§3), обобщающих на случай функций, определенных на последовательностях множеств, вытекают следующие две теоремы.
Теорема 1. Для каждого семейства  существует наименьшее существует наименьшее 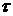 - аддитивное и - аддитивное и 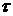 - мультипликативное семейство - мультипликативное семейство  , содержащее , содержащее  . .
Теорема 2. Для любых семейств  , ,  , , 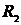 : :
 (1) (1)
 (2) (2)
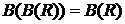 (3) (3)
Выполняя операции  и и  на последовательностях, члены которых принадлежат на последовательностях, члены которых принадлежат  , мы получаем множества, принадлежащие , мы получаем множества, принадлежащие  . Это позволяет произвести классификацию множеств, принадлежащих . Это позволяет произвести классификацию множеств, принадлежащих  : для произвольного семейства множеств : для произвольного семейства множеств  обозначим через обозначим через  семейство множеств вида семейство множеств вида  , где , где 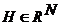 , и через , и через  семейство всех множеств вида семейство всех множеств вида 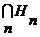 , где , где  . Очевидно, что . Очевидно, что  . .
Можно определить 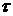 - аддитивное семейство как такое семейство, для которого - аддитивное семейство как такое семейство, для которого  , а , а 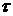 - мультипликативное как такое, для которого - мультипликативное как такое, для которого  . Т.к. семейство . Т.к. семейство  и и 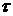 - аддитивно и - аддитивно и 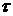 - мультипликативно, то - мультипликативно, то
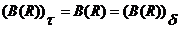 , ,
а т.к.  , то справедлива теорема. , то справедлива теорема.
|


 - некоторое фиксированное множество,
- некоторое фиксированное множество,  - функция произвольного числа переменных, каждое из которых пробегает какое-нибудь семейство подмножеств множества
- функция произвольного числа переменных, каждое из которых пробегает какое-нибудь семейство подмножеств множества  . Семейство
. Семейство  называется замкнутыми относительно
называется замкнутыми относительно  .
. существует такое семейство
существует такое семейство  , что
, что ,
, выполнены условия
выполнены условия ,
, 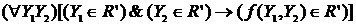 , (1)
, (1)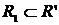 .
.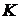 - множество всех семейств
- множество всех семейств  , т.к.
, т.к.  . Искомым семейством
. Искомым семейством  .
.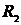 обладает этими свойствами, то из минимальности семейства
обладает этими свойствами, то из минимальности семейства  . Аналогично,
. Аналогично, 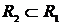 , т.к.
, т.к.  , мы будет обозначать это
, мы будет обозначать это  семейство
семейство 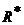 .
. ,
, 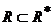 ,
, ,
, .
. замкнуто относительно
замкнуто относительно  . Для доказательства III заметим, что из условия I следует
. Для доказательства III заметим, что из условия I следует 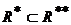 , с другой стороны,
, с другой стороны,  .
. . Наименьшее семейство множеств, содержащее
. Наименьшее семейство множеств, содержащее 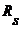 . Это семейство состоит из конечных сумм вида
. Это семейство состоит из конечных сумм вида  , где
, где  ,
,  и
и  - последовательность множеств, принадлежащих
- последовательность множеств, принадлежащих  .
.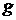 задаётся равенством
задаётся равенством  , то наименьшее семейство, содержащее
, то наименьшее семейство, содержащее  . Это семейство состоит из произведений вида
. Это семейство состоит из произведений вида  , где
, где 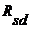 , причем
, причем  .
.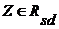 , т.е.
, т.е.  , где
, где 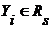 для
для  .
.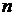 , что
, что 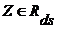 . Для
. Для 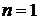 имеем
имеем 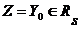 , а
, а 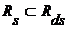 , т.к.
, т.к. 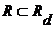 . Предположим, что теорема верна для
. Предположим, что теорема верна для 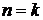 .
.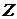 - произведение
- произведение 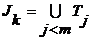 , где
, где  ,
,  и
и  для
для  . Обозначим
. Обозначим  . По предположению индукции
. По предположению индукции  и, значит,
и, значит, 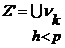 , где
, где  ,
,  и
и 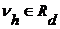 для
для  .
.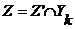 , то
, то  .
.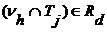 , получаем отсюда, что
, получаем отсюда, что  . Аналогично доказывается обратное включение.
. Аналогично доказывается обратное включение. ,
,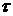 - аддитивные и
- аддитивные и  (соответственно
(соответственно 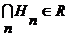 ) для каждой последовательности
) для каждой последовательности 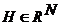 .
. , содержащее
, содержащее  (1)
(1) (2)
(2)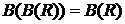 (3)
(3) и
и  на последовательностях, члены которых принадлежат
на последовательностях, члены которых принадлежат  семейство множеств вида
семейство множеств вида  , где
, где  семейство всех множеств вида
семейство всех множеств вида 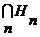 , где
, где  . Очевидно, что
. Очевидно, что  .
. , а
, а 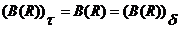 ,
,