
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Операции на бесконечных последовательностях множеств.Здесь вы рассмотрим один частный случай, когда область определения функции
Из формул (2) §1 непосредственно получаем:
где Кроме операций бесконечного сложения и умножения, рассмотрим ещё операции: 1) (ср. 2) (ср.
Легко видеть, что элемент Очевидно, что в силу (18) §1, гл. II:
Если знак включения в (2) можно заменить знаком равенства, т.е. если верхний и нижний пределы совпадают, то их общее значение обозначают Терминология эта аналогична терминологии, которой пользуются в теории вещественных чисел. Чтобы подчеркнуть эту аналогию, введем понятие характеристической функции данного множества. Пусть дано 1 и
Легко видеть, что для сходимости последовательности множеств  Понятие сходимости последовательности множеств обнаруживает очень интересные аналогии с классическими понятиями сходимости числовых последовательностей, если симметричную разность – двух множеств рассматривать как модуль разности двух чисел. Докажем, что условия
равносильны. В самом деле, условие (4) означает, что элемент
Пусть
откуда в силу (2) получаем (4'). Обратно, если выполнено условие (6) и Докажем ещё несколько более специальных правил, относящихся к перестановке символов Пусть функция
Докажем только первое из этих равенств, т.к. 2-е доказывается аналогично. Очевидно, что Справедлива также формула
В самом деле,
Если Полагая Тем же методом, что и (7) можно доказать равенства
Далее
В самом деле, Для доказательства обратного включения возьмём Из т.7 (§3, гл. III) следует, что существует такая последовательность
Выведем теперь из (7) – (10) формулу:
которая нам пригодится в гл. X. Здесь Заменяя
Таким образом, левая часть равенства (11) равна
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 254. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
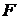 совпадает с
совпадает с 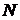 , т.е. функция
, т.е. функция  , или
, или  , или
, или 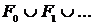 вместо
вместо 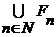 ;
; , или
, или  , или
, или  вместо
вместо  .
.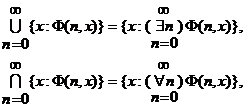 (1)
(1) - высказывательная функция 2х переменных, причем множество значений первой переменной (
- высказывательная функция 2х переменных, причем множество значений первой переменной (  ) ограничено множеством
) ограничено множеством 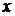 ) – некоторым множеством
) – некоторым множеством  .
. - верхний предел последовательности
- верхний предел последовательности 
 - наименьшая верхняя грань
- наименьшая верхняя грань  );
); - нижний предел последовательности
- нижний предел последовательности  - наибольшая нижняя грань
- наибольшая нижняя грань  тогда и только тогда, когда он принадлежит бесконечному числу множеств
тогда и только тогда, когда он принадлежит бесконечному числу множеств  , и
, и  тогда и только тогда, когда он принадлежит
тогда и только тогда, когда он принадлежит  (2)
(2) и называют пределом последовательности
и называют пределом последовательности 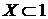 . Характеристической функцией множества
. Характеристической функцией множества  (3)
(3) .
.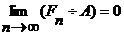 (4)
(4) (4')
(4') не более чем для конечного числа значений
не более чем для конечного числа значений  следует
следует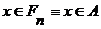 (5)
(5)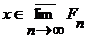 , т.е.
, т.е.  для бесконечного числа значений
для бесконечного числа значений  и
и  . Таким образом, из (4) следует
. Таким образом, из (4) следует , (6)
, (6) , то
, то 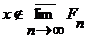 и тогда
и тогда  для
для  и
и  , и замене двух подряд идущих операций
, и замене двух подряд идущих операций 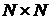 , функция
, функция  - на множестве
- на множестве 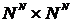 и
и  - на множестве
- на множестве  , причем значениями этих функций являются множества. Будем пользоваться символикой, введенной в §3, гл. III.
, причем значениями этих функций являются множества. Будем пользоваться символикой, введенной в §3, гл. III. ;
;  . (7)
. (7) , поэтому
, поэтому  . С другой стороны, если
. С другой стороны, если  , то
, то  для каких-то
для каких-то 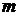 ,
, 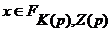 , где
, где 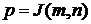 .
. (8)
(8) , поэтому
, поэтому  , откуда в силу произвольности
, откуда в силу произвольности 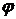 получаем
получаем .
.
 , то для каждого
, то для каждого  существует такое
существует такое 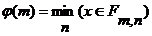 , получаем
, получаем 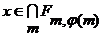 , следовательно
, следовательно  .
. (9)
(9)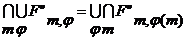 (º10)
(º10) , поэтому
, поэтому  , откуда
, откуда  .
. и положим далее
и положим далее  . Т.к.
. Т.к.  для каждого
для каждого  для семейства всех множеств
для семейства всех множеств 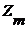 . Полагая
. Полагая  , получаем, что
, получаем, что  и
и  для каждого
для каждого  , что
, что  для каждого
для каждого 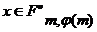 для каждого
для каждого  .
. , (º11)
, (º11) - функция 4-х переменных, определенная на декартовом произведении
- функция 4-х переменных, определенная на декартовом произведении  , а значениями её являются множества.
, а значениями её являются множества. в равенстве (º10) на
в равенстве (º10) на  (где
(где 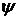 - произвольная, но фиксированная последовательность), получаем
- произвольная, но фиксированная последовательность), получаем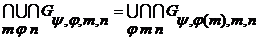 .
. . С помощью (7) и (9) получаем из этого выражения правую часть равенства (11).
. С помощью (7) и (9) получаем из этого выражения правую часть равенства (11).