
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 4 (обобщённые законы дистрибутивности).Если
Д о к а з а т е л ь с т в о. Пусть
Т.к.
Для того, чтобы доказать обратно включением, возьмём
Положим
Если
Таким образом, мы показали, что для произвольных a из (23) следует (25), т.е.
Отсюда в силу (22) имеем равенство (20). Для доказательства (21) заменим в (20)
Применяя законы де Моргана (8) и (9) и формулу Теперь обобщим формулы (1) – (4), §7, гл. II, характеризующие образы и прообразы конечных сумм и произведений, на бесконечные суммы и произведения. Теорема 5. Пусть
Если Д о к а з а т е л ь с т в о. Из определения образа получаем
Аналогично, используя (18) (§1, гл. II), получаем для (27):
Если
Откуда в силу (2) (§7, гл. II):
Т.к. обратное включение (27) также выполняется, то теорема доказана. Теорема 6. Если
Д о к а з а т е л ь с т в о. Из определения прообраза (§7, гл. II) получаем Аналогично доказывается (23): 
Равенства (26) и (28) означают, что операции взятия образа и прообраза аддитивны, а равенство (29) – что операция взятия прообраза ещё и мультипликативна лишь для взаимно однозначных функций. Рассмотрим несколько примеров. Пусть множество 1 будет топологическим пространством (§8, гл. I). Пример 1. Если значения функции Д о к а з а т е л ь с т в о. Т.к. Пример 2. Если значения функции Д о к а з а т е л ь с т в о. Множества Пример 3. Если значения функции Д о к а з а т е л ь с т в о. Очевидно, что Т.к. Следовательно, Пример 4. Если значения функции Д о к а з а т е л ь с т в о. Обозначим Применяя формулу (15), §8, гл. I, получим Наконец, если Пример 5. В связи с теоремами, сформулированными в примерах 1 и 2, можно определить топологическое пространство, беря в качестве первичного понятия, вместо понятия замыкания, понятия замкнутого множества или открытого множества. А именно под топологическим пространством будет понимать множество, в котором выделено некоторое семейство I. Если II. Если семейство Если в качестве первичного понятия взять понятие открытого множества, а, обозначая через I '. Если II '. Если семейство
Система аксиом (I) – (II) эквивалентна системе (1) – (4) гл. I, §8. Последняя выполняется, если определить Аналогичное замечания относится к системе аксиом (I ') – (II'). Пример 6. Замкнутой базой топологического пространства называют такое семейство Замкнутой подбазой называется каждое такое семейство Пример 7. Открытая база и открытая подбаза определяются аналогично – заменой
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 264. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , то
, то (20)
(20) (21)
(21) и
и  . По определению семейства
. По определению семейства 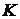 множество
множество  , т.е. существует
, т.е. существует  . Согласно (3)
. Согласно (3) 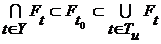 . Т.к. это верно для любого
. Т.к. это верно для любого  ), то в силу теоремы 1 имеем:
), то в силу теоремы 1 имеем: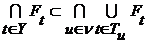 .
. (22)
(22) (23)
(23) (24)
(24)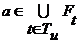 . Значит, существует такое
. Значит, существует такое  , что
, что  . Поэтому
. Поэтому  , откуда
, откуда  , т.е.
, т.е. 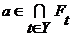 и
и (25)
(25)
 на
на  , где
, где  :
:
 , получаем (21).
, получаем (21). и
и 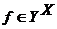 . Тогда
. Тогда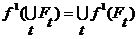 (26)
(26)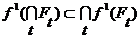 (27)
(27) - взаимно однозначная функция, то знак включения в (27) можно заменить знаком равенства.
- взаимно однозначная функция, то знак включения в (27) можно заменить знаком равенства.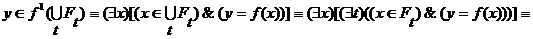
 , откуда следует равенство (26).
, откуда следует равенство (26).
 и что т.д.
и что т.д.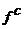 и множествам
и множествам  получаем
получаем

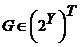 и
и  (28)
(28) (29)
(29) .
. .
.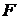 - замкнутые множества (§8, гл. I), то произведение
- замкнутые множества (§8, гл. I), то произведение  также замкнуто.
также замкнуто. , то
, то  для каждого
для каждого  , откуда
, откуда 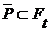 , поскольку
, поскольку 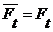 . Тогда
. Тогда  , а т.к. и
, а т.к. и  (аксиома 3, §8, гл. I), то
(аксиома 3, §8, гл. I), то 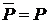 .
. - открытое множество, то сумма
- открытое множество, то сумма  также открыта.
также открыта. замкнуты, поэтому и произведение
замкнуты, поэтому и произведение  замкнуто. Согласно закону де Моргана (9), множество
замкнуто. Согласно закону де Моргана (9), множество  также замкнуто, а это значит, что множество
также замкнуто, а это значит, что множество 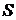 открыто.
открыто. - регулярно замкнутые множества (§9, гл. I), то множество
- регулярно замкнутые множества (§9, гл. I), то множество  также регулярно замкнуто и содержит в качестве подмножеств все множества
также регулярно замкнуто и содержит в качестве подмножеств все множества  . Каждое регулярно замкнутое множество, содержащее в качестве подмножеств все множества
. Каждое регулярно замкнутое множество, содержащее в качестве подмножеств все множества 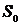 .
.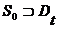 , откуда
, откуда  и
и  . (
. (  )
) и
и  . В то же время
. В то же время  и поэтому
и поэтому 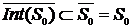 .
. , т.е. множество
, т.е. множество 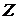 - регулярно замкнутое множество и
- регулярно замкнутое множество и  для каждого
для каждого  и тогда
и тогда  .
.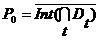 также регулярно замкнуто и содержится в каждом из множеств
также регулярно замкнуто и содержится в каждом из множеств  .
. . Тогда
. Тогда  , поэтому
, поэтому  .
. . Таким образом,
. Таким образом,  , то
, то  и
и  , т.е.
, т.е.  для каждого
для каждого  для каждого
для каждого  . Поэтому
. Поэтому 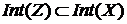 и
и  .
. , то
, то  (т.е. (см. (9), §8, гл. I) произведение любого непустого семейства замкнутых множеств замкнуто).
(т.е. (см. (9), §8, гл. I) произведение любого непустого семейства замкнутых множеств замкнуто).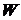 конечно и
конечно и  (т.е. (см. (1), §8, гл. I) сумма конечного числа замкнутых множеств замкнута).
(т.е. (см. (1), §8, гл. I) сумма конечного числа замкнутых множеств замкнута). , то
, то  .
. .
.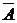 формулой
формулой  , где
, где 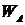 - семейство всех замкнутых множеств, содержащих
- семейство всех замкнутых множеств, содержащих 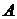 . Тогда
. Тогда  .
. , что для каждого
, что для каждого  существует непустое семейство
существует непустое семейство 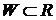 , для которого
, для которого 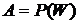 .
. образует замкнутую базу.
образует замкнутую базу.