
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГЛАВА IV. БЕСКОНЕЧНЫЕ СУММЫ, ПРОИЗВЕДЕНИЯ И ДЕКАРТОВЫ ПРОИЗВЕДЕНИЯ.
В этой главе, как и в предыдущих, мы берем за основу систему аксиом ∑º, причем теоремы не помеченные знаком º, не зависят от аксиом выбора. Цель настоящей главы – обобщить операции сложения, умножения и декартова умножения на произведение семейства множеств.
Бесконечные суммы и произведения.
Пусть Тогда Пусть Сумма множеств
Очевидно, что Если
Если же
Таким образом, рассматриваемые здесь понятия обобщают понятия суммы и произведения множеств на случай произвольного семейства слагаемых. Из (1) вытекают равенства: Справедливые для каждой высказывательной функции 2х переменных В самом деле, полагая
2-е равенство в (2) доказывается аналогично. Используя (1) и формулы, характеризующие кванторы, §1 гл.II, получаем следующие законы для обобщённых операций:

Все эти законы непосредственно следуют из соответствующих законов §1, гл. II. Докажем, например, закон де Моргана (8):
Для доказательства использованы следующие формулы: (2) §2, гл. I: (5) §1, гл. II: Диаграмма, приведенная в гл.II, §1, позволяет получить дополнительные законы для бесконечных операций. Для этого достаточно знак импликации В частности, получаем следующую важную формулу:
Вообще говоря, знак включения здесь нельзя заменить обратным (см. (18) гл.II, §1). Теорема 1. Сумма
Произведение
Другими словами, сумма Д о к а з а т е л ь с т в о. Из (3) и (13) следует, что сумма Но т.к. по условию теоремы Доказательство для произведения аналогично. Теорема 2 (Обобщённые законы ассоциативности). Если
Д о к а з а т е л ь с т в о. Полагая представим (17) в виде:
Имеем Обратно, пусть Теорема 3 (обобщенные законы коммутативности). Если
Д о к а з а т е л ь с т в о. Докажем (17'). Пусть |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 262. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
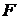 - функция, значениями которой являются подмножества некоторого фиксированного множества
- функция, значениями которой являются подмножества некоторого фиксированного множества  , а область её определения – непустое множество
, а область её определения – непустое множество 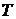 . (
. (  )
) . Вместо
. Вместо 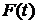 мы будем писать
мы будем писать 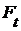 .
.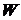 - множество значений функций
- множество значений функций  пробегает все
пробегает все  , а произведение -
, а произведение -  , т.е.
, т.е. ,
, 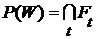
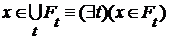 ,
, 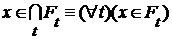 (1)
(1)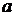 , то
, то .
. , то
, то ,
,  .
.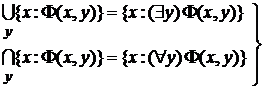 (2)
(2) (с ограниченной областью определения).
(с ограниченной областью определения). , получаем
, получаем  , поэтому:
, поэтому:
 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)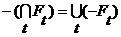 (8)
(8) , (9)
, (9)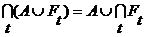 (10)
(10)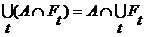 , (11)
, (11) , (12)
, (12) . (13)
. (13)
 ,
, .
.
 заменить знаком включения
заменить знаком включения 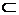 , а функцию
, а функцию 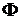 заменить функцией 2-х переменных
заменить функцией 2-х переменных  (14)
(14) - единственное множество
- единственное множество 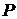 , удовлетворяющее условиям
, удовлетворяющее условиям (15)
(15) (16)
(16) - единственное множество
- единственное множество 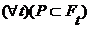 (15')
(15')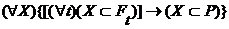 (16')
(16') , а произведение
, а произведение 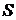 удовлетворяет этим условиям, то из (15) и (13) непосредственно следует, что
удовлетворяет этим условиям, то из (15) и (13) непосредственно следует, что 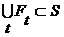 . Подставляя
. Подставляя 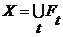 в (16) и используя (3), получаем, что
в (16) и используя (3), получаем, что  .
. .
. , где
, где 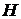 - функция с областью определения
- функция с областью определения  , значениями которой являются множества (т.е.
, значениями которой являются множества (т.е.  ), то
), то , (17)
, (17) (18)
(18) и
и  ,
, (19)
(19)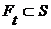 для каждого
для каждого  и, в частности, для каждого
и, в частности, для каждого  , откуда по теореме 1
, откуда по теореме 1 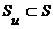 .
. для производного
для производного  . Для каждого
. Для каждого 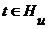 , откуда
, откуда  и, значит,
и, значит,  . Т.к. это верно для любого
. Т.к. это верно для любого  . Применяя теорему 1 получаем (19). Равенство (18) доказывается аналогично.
. Применяя теорему 1 получаем (19). Равенство (18) доказывается аналогично.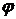 - перестановка множества
- перестановка множества  (17')
(17') (18')
(18')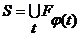 . Если
. Если  . А т.к.
. А т.к.  для
для  . Обратно, если
. Обратно, если  , поскольку
, поскольку  . Отсюда
. Отсюда