Следствие 11. Множество значений бесконечной последовательности с попарно различными членами бесконечно.
Действительно, такое множество является взаимно однозначным образом множества 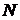 . Если бы оно было конечным, то по теореме 1 и . Если бы оно было конечным, то по теореме 1 и 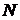 было бы конечным. Из этого следствия и теоремы 8 вытекает следующая теорема. было бы конечным. Из этого следствия и теоремы 8 вытекает следующая теорема.
Теорема 12. Множество, служащее в качестве подмножества множество значений бесконечной последовательности с попарно различными членами, бесконечно.
Множество, удовлетворяющее условиям теоремы 12, называется бесконечным в смысле Дедекинда.
Множество, бесконечное в смысле Дедекинда, бесконечно – аналог теоремы 12.
Обратная теорема также верна, но для её доказательства требуется аксиома выбора.
°Теорема 13. Бесконечное множество бесконечно в смысле Дедекинда.
Д о к а з а т е л ь с т в о. Пусть  - бесконечное множество и - бесконечное множество и
 - функция выбора для семейства - функция выбора для семейства  - - 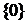 . .
Продолжим  , полгая , полгая  , где , где 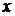 - произвольный фиксированный элемент множества - произвольный фиксированный элемент множества  . Таким образом, . Таким образом,  ставит в соответствие каждому подмножеству множества ставит в соответствие каждому подмножеству множества  элемент множества элемент множества  и и  , если , если  . .
Определим теперь по индукции последовательность  и и  : :
 , , 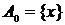
 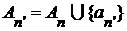
Легко показать по индукции, что любое множество 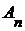 конечно и конечно и 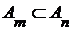 для для 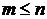 . Отсюда следует, что . Отсюда следует, что  и, значит, и, значит,  и и  для каждого для каждого 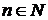 . В последовательности . В последовательности 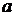 все члены попарно различны. все члены попарно различны.
В самом деле, если  , то , то  , но , но  , т.к. полагая , т.к. полагая 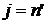 , получаем , получаем 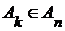 и и 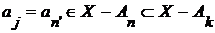 . Поэтому . Поэтому 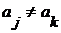 . .
Множество  поэтому бесконечно в смысле Дедекинда, ибо оно содержит подмножество поэтому бесконечно в смысле Дедекинда, ибо оно содержит подмножество 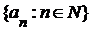 , которое является множеством значений бесконечной последовательности с попарно различными членами. , которое является множеством значений бесконечной последовательности с попарно различными членами.
Теорема Д. Кёнига.
Пусть 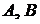 - множества, - множества,  и и  . Конечная последовательность . Конечная последовательность  (бесконечная последовательность (бесконечная последовательность  ) называется ветвью длины ) называется ветвью длины  (бесконечной ветвью), если (бесконечной ветвью), если  и и  для каждого для каждого 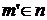 (для каждого (для каждого 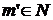 ). ).
Элемент  (не обязательно принадлежащий (не обязательно принадлежащий  ) называется начальной вершиной ветви. ) называется начальной вершиной ветви.
Если  - ветвь длины - ветвь длины  (бесконечная ветвь) и (бесконечная ветвь) и  ( (  ), то ), то  - ветвь длины - ветвь длины 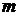 . .
Теорема 1 (Д. Кёниг, 1927г.). Пусть все множества уровня функции  конечны. Если конечны. Если  и для каждого и для каждого 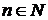 существует ветвь длины существует ветвь длины  с начальной вершиной с начальной вершиной 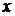 , то существует по крайней мере одна бесконечная ветвь с начальной вершиной , то существует по крайней мере одна бесконечная ветвь с начальной вершиной 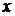 . .
Д о к а з а т е л ь с т в о. Обозначим через 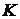 множество таких элементов множество таких элементов  , что для каждого , что для каждого 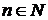 существует ветвь длины существует ветвь длины  с начальной вершиной с начальной вершиной 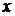 . Очевидно, что . Очевидно, что  . .
Лемма 1. Если  , то , то  . .
Действительно, предположим обратное, т.е. что  , и будем считать конечное множество , и будем считать конечное множество 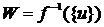 множеством значений некоторой последовательности множеством значений некоторой последовательности 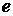 длины длины 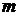 . Тогда для каждого . Тогда для каждого  найдется такое число найдется такое число 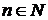 , что не существует ветви длины , что не существует ветви длины  с начальной вершиной с начальной вершиной  . Наименьшее число . Наименьшее число  , обладающее этим свойством, обозначим через , обладающее этим свойством, обозначим через 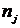 и положим и положим  . Тогда . Тогда  для всех для всех  , и, значит, ни для одного элемента , и, значит, ни для одного элемента  множества уровня функции множества уровня функции  нет ветви, имеющей длину нет ветви, имеющей длину  и начальную вершину и начальную вершину  . С другой стороны, из условия . С другой стороны, из условия  следует, что существует ветвь следует, что существует ветвь 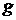 , имеющая длину , имеющая длину  и начальную вершину и начальную вершину  . Полагая . Полагая  для для  , получаем ветвь длиной , получаем ветвь длиной  с начальной вершиной с начальной вершиной  , что ведет к противоречию, т.к. , что ведет к противоречию, т.к.  . .
Теперь пусть 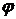 - функция выбора для семейства непустых множеств вида - функция выбора для семейства непустых множеств вида 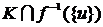 , ,  . Дополним область определения функции . Дополним область определения функции 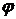 , полагая , полагая  . Тогда . Тогда 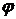 ставит соответствие каждому множеству вида ставит соответствие каждому множеству вида 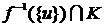 элемент множества элемент множества 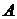 . Определим по индукции последовательность . Определим по индукции последовательность  : :
 , ,
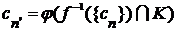 . .
Покажем, что для каждого 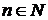
 (1) (1)
Действительно, для 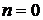 имеем имеем  , значит, , значит,  и, согласно лемме 1, и, согласно лемме 1,  . Следовательно, по определению функции выбора . Следовательно, по определению функции выбора 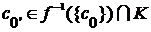 . Если утверждение (1) верно для какого-то . Если утверждение (1) верно для какого-то 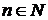 , то по лемме 1: , то по лемме 1:  и, значит, и, значит,  . Таким образом, утверждение (1) доказано. Из него следует, что . Таким образом, утверждение (1) доказано. Из него следует, что  , т.е. , т.е.  - бесконечная ветвь с начальной вершиной - бесконечная ветвь с начальной вершиной 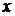 . .
Мы использовали здесь факт существования функции выбора, т.е. мы воспользовались аксиомой выбора. Отметим, кстати, что мы использовали не саму аксиому выбора, а только один её частный случай, утверждающий существование функции выбора для произвольного семейства конечных множеств. Анализ приведенного доказательства показывает, что достаточно принять существование функции выбора лишь для счетных семейств конечных множеств.
Можно доказать, что полностью устроить аксиому выбора из доказательства теоремы Кёнига невозможно, т.е. что эта теорема не следует из системы аксиом 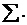
Пример. Пусть 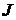 - замкнутый интервал - замкнутый интервал 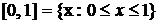 , и пусть , и пусть  для для  , , 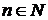 . .
Пусть  - такое семейство открытых интервалов, что - такое семейство открытых интервалов, что  . Говорят, что . Говорят, что  покрывает интервал покрывает интервал 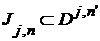 . .
Теорема 2. Существует такое число  , что , что  покрывает все интервалы покрывает все интервалы 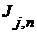 для для  . .
Д о к а з а т е л ь с т в о. Пусть 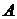 - семейство всех интервалов - семейство всех интервалов 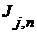 , а , а  - семейство тех интервалов - семейство тех интервалов 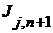 , , 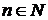 , которые не покрываются , которые не покрываются  . .
Пусть  - тот интервал - тот интервал  , который содержит , который содержит 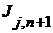 . Тогда определена функция, принадлежащая . Тогда определена функция, принадлежащая  , причем множества её уровня конечны. Для доказательства теоремы достаточно показать, что существует такое число , причем множества её уровня конечны. Для доказательства теоремы достаточно показать, что существует такое число  , что ни одна из ветвей с начальной вершиной , что ни одна из ветвей с начальной вершиной 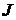 не имеет длины не имеет длины  . .
Предположим обратное. Тогда по теореме Кёнига существует бесконечная ветвь, т.е. такая последовательность интервалов 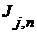 , что каждый следующий содержится в предыдущем и ни один из них не накрывается , что каждый следующий содержится в предыдущем и ни один из них не накрывается  . .
Пусть 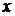 - общая точка всех интервалов этой последовательности. Т.к. - общая точка всех интервалов этой последовательности. Т.к.  , то в , то в  существует такой интервал существует такой интервал  , что , что 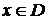 . Отсюда легко следует, что . Отсюда легко следует, что 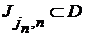 для некоторого для некоторого  , и, значит, , и, значит,  покрывает покрывает  , что противоречит определению этого интервала. , что противоречит определению этого интервала.
Графы. Теорема Рамсея.
Множество  , состоящее из неупорядоченных пар различных элементов, называется графом. Множество , состоящее из неупорядоченных пар различных элементов, называется графом. Множество  называется полем графа, его элементы – вершинами графа. называется полем графа, его элементы – вершинами графа.
Если  , то пара , то пара  называется ребром графа. Говорят также, что вершины называется ребром графа. Говорят также, что вершины 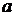 и и  в графе в графе  связаны ребром. Такая терминология объясняется геометрической интерпретацией графа в случае, когда его поле состоит из конечного числа линейно независимых точек пространства связаны ребром. Такая терминология объясняется геометрической интерпретацией графа в случае, когда его поле состоит из конечного числа линейно независимых точек пространства  . .
 Эта геометрическая интерпретация представляет собой линию, отрезки которой (рёбра) не имеют общих точке, за исключением вершин. Эта геометрическая интерпретация представляет собой линию, отрезки которой (рёбра) не имеют общих точке, за исключением вершин.
Графом является, например, множество всех пар  , где , где 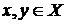 и и  . Этот граф будем обозначать символом . Этот граф будем обозначать символом  и называть полным графом над полем и называть полным графом над полем  . .
Если  - граф над полем - граф над полем  , то разность , то разность 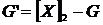 также является графом, называемым дополнением графа также является графом, называемым дополнением графа  . .
Граф 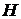 называется подграфом графа называется подграфом графа  , если , если  . Изучение графов равносильно изучению симметричных антирефлексивных отношений, т.е. отношений, для которых 1) . Изучение графов равносильно изучению симметричных антирефлексивных отношений, т.е. отношений, для которых 1)  , 2) , 2)  . .
В самом деле, каждому графу  можно поставить в соответствие такое отношение, полагая можно поставить в соответствие такое отношение, полагая 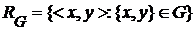 . И обратно, каждое симметричное антирефлексивное отношение определяет граф . И обратно, каждое симметричное антирефлексивное отношение определяет граф  , причем , причем  . .
Теорема (Рамсей, 1923г). Если  - граф над бесконечным полем, то или - граф над бесконечным полем, то или  , или , или  содержит полный подграф над бесконечным полем. содержит полный подграф над бесконечным полем.
Д о к а з а т е л ь с т в о. Пусть  - функция выбора для - функция выбора для  . Положим . Положим
 , ,
 . .
Тогда множество  состоит из вершин, связанных ребром с состоит из вершин, связанных ребром с 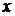 в графе в графе  , а , а  - из вершин, связанных ребром с - из вершин, связанных ребром с 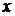 в графе в графе  . .
Определим по индукции 4 последовательности:
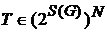 , ,  , ,
 , , 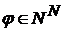 . .
А именно:
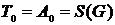 , ,  , ,  . .
1) 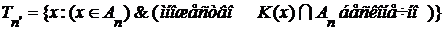
2)  , ,  , ,  . .
Рассмотрим 2 случая:
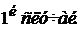  для всех для всех 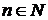 . .
Можно доказать по индукции, что для всех 
(1)  , ,
(2) множество  бесконечно, бесконечно,
(3)  , ,
(4)  . .
Если  , то из (3) следует, что , то из (3) следует, что  , а т.к. , а т.к. 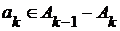 (по (1) и (4)), то (по (1) и (4)), то  . .
Поскольку множество значений последовательности 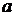 бесконечно, полный граф, полем которого является это множество, содержится в бесконечно, полный граф, полем которого является это множество, содержится в  , и теорема доказана. , и теорема доказана.
2-й случай. Существует такое  , что , что  . Обозначим наименьшее такое число через . Обозначим наименьшее такое число через 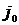 . Т.к. . Т.к. 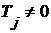 для для  , то , то  . .
Множество  или равно или равно  (если (если  ), или имеет вид ), или имеет вид  . В обоих случаях оно бесконечно: в 1-м случае – по условию, во 2-м случае – поскольку . В обоих случаях оно бесконечно: в 1-м случае – по условию, во 2-м случае – поскольку  . .
Определим по индукции последовательность  подмножеств множества подмножеств множества  и последовательность и последовательность  элементов множества элементов множества  : :
 , ,  , ,
 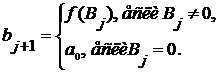
Множества  образуют убывающую последовательность: образуют убывающую последовательность:  для для  . Докажем по индукции, что каждое множество . Докажем по индукции, что каждое множество  бесконечно. бесконечно.
1) Действительно,  бесконечно. Пусть утверждение верно для некоторого бесконечно. Пусть утверждение верно для некоторого  . Докажем, что множество . Докажем, что множество 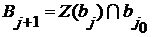 также бесконечно. Если бы оно было конечным, то для каждого также бесконечно. Если бы оно было конечным, то для каждого  было бы было бы  , а тогда множество , а тогда множество  и тем более и тем более  было бы бесконечным, откуда следовало бы, что было бы бесконечным, откуда следовало бы, что  , вопреки тому, что , вопреки тому, что  пусто. пусто.
Итак, каждое множество  бесконечно. Отсюда следует, что бесконечно. Отсюда следует, что  для всех для всех  . Если . Если  , то , то  , а потому , а потому  . Беря в качестве . Беря в качестве  множество всех значений последовательности множество всех значений последовательности  , получаем , получаем  , и, таким образом, теорема доказана, т.к. множество , и, таким образом, теорема доказана, т.к. множество  бесконечно. бесконечно.
Пример. Пусть  , и пусть , и пусть  -множество таких неупорядоченных пар -множество таких неупорядоченных пар  , что , что 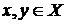 и числа и числа  взаимно просты. Применяя теорему Рамсея, получим, что если взаимно просты. Применяя теорему Рамсея, получим, что если  - бесконечно, то оно содержит либо такое бесконечное подмножество - бесконечно, то оно содержит либо такое бесконечное подмножество  , что каждые два числа, принадлежащие , что каждые два числа, принадлежащие  , взаимно просты, либо такое бесконечное подмножество , взаимно просты, либо такое бесконечное подмножество  , что никакие два числа, принадлежащие , что никакие два числа, принадлежащие  , не взаимно просты. , не взаимно просты.
Замечание 1. Наглядно теорему Рамсея можно сформулировать следующим образом: если каждое из ребер полного графа  , где , где  - бесконечное множество, выкрасить в один их 2-х цветов, то - бесконечное множество, выкрасить в один их 2-х цветов, то  будет содержать такое бесконечное множество будет содержать такое бесконечное множество  , что все ребра графа , что все ребра графа  будут выкрашены в один и тот же цвет. будут выкрашены в один и тот же цвет.
Замечание 2. Теорема Рамсея имеет свой аналог (ниже принадлежащий Рамсею) для конечных множеств:
Для любого натурального числа  найдётся такое натуральное число найдётся такое натуральное число 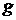 , что если множество , что если множество  имеет менее имеет менее 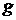 элементов, то для каждого графа элементов, то для каждого графа  существует такое подмножество существует такое подмножество  , содержащее , содержащее  элементов, что элементов, что  или или  . .
Другими словами, если  - граф над - граф над 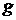 -элементным полем, то или -элементным полем, то или  , или , или  содержит полный подграф над содержит полный подграф над  -элементным полем. -элементным полем.
|


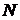 . Если бы оно было конечным, то по теореме 1 и
. Если бы оно было конечным, то по теореме 1 и  - бесконечное множество и
- бесконечное множество и - функция выбора для семейства
- функция выбора для семейства  -
- 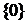 .
. , где
, где 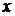 - произвольный фиксированный элемент множества
- произвольный фиксированный элемент множества  , если
, если  .
. и
и  :
: ,
, 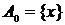

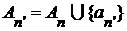
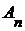 конечно и
конечно и 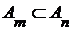 для
для 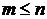 . Отсюда следует, что
. Отсюда следует, что  и, значит,
и, значит,  и
и  для каждого
для каждого 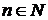 . В последовательности
. В последовательности 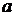 все члены попарно различны.
все члены попарно различны. , то
, то  , но
, но  , т.к. полагая
, т.к. полагая 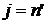 , получаем
, получаем 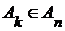 и
и 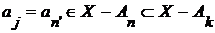 . Поэтому
. Поэтому 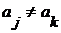 .
.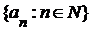 , которое является множеством значений бесконечной последовательности с попарно различными членами.
, которое является множеством значений бесконечной последовательности с попарно различными членами.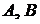 - множества,
- множества,  и
и  . Конечная последовательность
. Конечная последовательность  (бесконечная последовательность
(бесконечная последовательность  ) называется ветвью длины
) называется ветвью длины  (бесконечной ветвью), если
(бесконечной ветвью), если  и
и  для каждого
для каждого 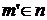 (для каждого
(для каждого 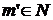 ).
). (не обязательно принадлежащий
(не обязательно принадлежащий  ) называется начальной вершиной ветви.
) называется начальной вершиной ветви. - ветвь длины
- ветвь длины  (
(  ), то
), то  - ветвь длины
- ветвь длины 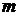 .
. и для каждого
и для каждого 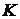 множество таких элементов
множество таких элементов  , что для каждого
, что для каждого  .
. , то
, то  .
. , и будем считать конечное множество
, и будем считать конечное множество 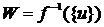 множеством значений некоторой последовательности
множеством значений некоторой последовательности 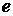 длины
длины  найдется такое число
найдется такое число  . Наименьшее число
. Наименьшее число 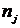 и положим
и положим  . Тогда
. Тогда  для всех
для всех  множества уровня функции
множества уровня функции  нет ветви, имеющей длину
нет ветви, имеющей длину  и начальную вершину
и начальную вершину 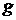 , имеющая длину
, имеющая длину  и начальную вершину
и начальную вершину  . Полагая
. Полагая  для
для  , получаем ветвь длиной
, получаем ветвь длиной  , что ведет к противоречию, т.к.
, что ведет к противоречию, т.к.  .
.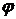 - функция выбора для семейства непустых множеств вида
- функция выбора для семейства непустых множеств вида 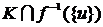 ,
,  . Тогда
. Тогда 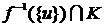 элемент множества
элемент множества 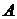 . Определим по индукции последовательность
. Определим по индукции последовательность  ,
,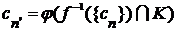 .
. (1)
(1)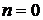 имеем
имеем  и, согласно лемме 1,
и, согласно лемме 1,  . Следовательно, по определению функции выбора
. Следовательно, по определению функции выбора 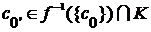 . Если утверждение (1) верно для какого-то
. Если утверждение (1) верно для какого-то  и, значит,
и, значит,  . Таким образом, утверждение (1) доказано. Из него следует, что
. Таким образом, утверждение (1) доказано. Из него следует, что  , т.е.
, т.е. 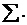
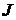 - замкнутый интервал
- замкнутый интервал 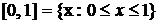 , и пусть
, и пусть  для
для  ,
,  - такое семейство открытых интервалов, что
- такое семейство открытых интервалов, что  . Говорят, что
. Говорят, что  .
. для
для  .
. - семейство тех интервалов
- семейство тех интервалов  ,
,  - тот интервал
- тот интервал  , который содержит
, который содержит  , причем множества её уровня конечны. Для доказательства теоремы достаточно показать, что существует такое число
, причем множества её уровня конечны. Для доказательства теоремы достаточно показать, что существует такое число  , то в
, то в  , что
, что 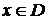 . Отсюда легко следует, что
. Отсюда легко следует, что 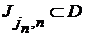 для некоторого
для некоторого  , что противоречит определению этого интервала.
, что противоречит определению этого интервала. называется полем графа, его элементы – вершинами графа.
называется полем графа, его элементы – вершинами графа. , то пара
, то пара  называется ребром графа. Говорят также, что вершины
называется ребром графа. Говорят также, что вершины  .
. Эта геометрическая интерпретация представляет собой линию, отрезки которой (рёбра) не имеют общих точке, за исключением вершин.
Эта геометрическая интерпретация представляет собой линию, отрезки которой (рёбра) не имеют общих точке, за исключением вершин. , где
, где 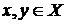 и
и  . Этот граф будем обозначать символом
. Этот граф будем обозначать символом  и называть полным графом над полем
и называть полным графом над полем 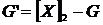 также является графом, называемым дополнением графа
также является графом, называемым дополнением графа 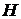 называется подграфом графа
называется подграфом графа  . Изучение графов равносильно изучению симметричных антирефлексивных отношений, т.е. отношений, для которых 1)
. Изучение графов равносильно изучению симметричных антирефлексивных отношений, т.е. отношений, для которых 1)  , 2)
, 2)  .
.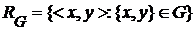 . И обратно, каждое симметричное антирефлексивное отношение определяет граф
. И обратно, каждое симметричное антирефлексивное отношение определяет граф  , причем
, причем  .
. содержит полный подграф над бесконечным полем.
содержит полный подграф над бесконечным полем. . Положим
. Положим ,
, .
. состоит из вершин, связанных ребром с
состоит из вершин, связанных ребром с  - из вершин, связанных ребром с
- из вершин, связанных ребром с 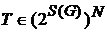 ,
,  ,
, ,
, 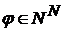 .
.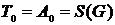 ,
,  ,
,  .
.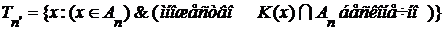
 ,
,  ,
,  .
.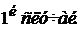
 для всех
для всех  ,
, бесконечно,
бесконечно, ,
, .
. , то из (3) следует, что
, то из (3) следует, что  , а т.к.
, а т.к. 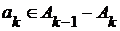 (по (1) и (4)), то
(по (1) и (4)), то  .
. , что
, что  . Обозначим наименьшее такое число через
. Обозначим наименьшее такое число через 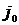 . Т.к.
. Т.к. 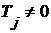 для
для  , то
, то  .
. или равно
или равно  ), или имеет вид
), или имеет вид  . В обоих случаях оно бесконечно: в 1-м случае – по условию, во 2-м случае – поскольку
. В обоих случаях оно бесконечно: в 1-м случае – по условию, во 2-м случае – поскольку  .
. ,
,  ,
,
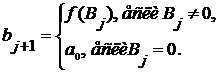
 образуют убывающую последовательность:
образуют убывающую последовательность:  для
для  . Докажем по индукции, что каждое множество
. Докажем по индукции, что каждое множество  бесконечно. Пусть утверждение верно для некоторого
бесконечно. Пусть утверждение верно для некоторого 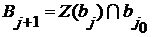 также бесконечно. Если бы оно было конечным, то для каждого
также бесконечно. Если бы оно было конечным, то для каждого  было бы
было бы  , а тогда множество
, а тогда множество  и тем более
и тем более  было бы бесконечным, откуда следовало бы, что
было бы бесконечным, откуда следовало бы, что  , вопреки тому, что
, вопреки тому, что  пусто.
пусто. для всех
для всех  , то
, то  , а потому
, а потому  . Беря в качестве
. Беря в качестве  множество всех значений последовательности
множество всех значений последовательности  , и, таким образом, теорема доказана, т.к. множество
, и, таким образом, теорема доказана, т.к. множество  , и пусть
, и пусть  взаимно просты. Применяя теорему Рамсея, получим, что если
взаимно просты. Применяя теорему Рамсея, получим, что если  , что никакие два числа, принадлежащие
, что никакие два числа, принадлежащие  , где
, где  будут выкрашены в один и тот же цвет.
будут выкрашены в один и тот же цвет. существует такое подмножество
существует такое подмножество  , содержащее
, содержащее  или
или  .
.