Конечные и бесконечные множества.
Понятия, введённые в §1 и §2, позволяют вывести из аксиом теории множеств основные свойства конечных и бесконечных множеств.
О п р е д е л е н и е. Говорят, что множество  имеет имеет  элементов элементов  , и пишут , и пишут  , если существует последовательность с , если существует последовательность с  попарно различными членами и множеством значений попарно различными членами и множеством значений  (Она называется взаимно однозначной последовательностью с (Она называется взаимно однозначной последовательностью с  членами). членами).
Множество  называют конечным, если называют конечным, если  для некоторого для некоторого  ; в противном случае оно называется бесконечным. ; в противном случае оно называется бесконечным.
Множество  имеет 0 элементов тогда и только тогда, когда имеет 0 элементов тогда и только тогда, когда  , т.к. единственной последовательностью с 0 членами является пустая последовательность. , т.к. единственной последовательностью с 0 членами является пустая последовательность.
Для каждого  множество множество  имеет имеет  элементов. Действительно, функция Jp, заданная формулой Jp(x)=x для каждого элементов. Действительно, функция Jp, заданная формулой Jp(x)=x для каждого  , является, согласно определению последовательности, последовательностью с , является, согласно определению последовательности, последовательностью с  попарно различными членами и множеством значений попарно различными членами и множеством значений  . .
Теорема 1. Если функция  взаимно однозначно отображает множество взаимно однозначно отображает множество  на на  , то условия , то условия  и и  эквивалентны. эквивалентны.
Д о к а з а т е л ь с т в о. Если 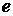 - последовательность с - последовательность с  попарно различными членами и множеством значений попарно различными членами и множеством значений  , то , то  - последовательность с - последовательность с  попарно различными членами (см. теорему 2 §6, гл.II) и множеством значений попарно различными членами (см. теорему 2 §6, гл.II) и множеством значений  . .
Лемма. Если  - взаимно однозначная функция, - взаимно однозначная функция, 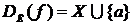 , , 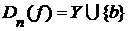 и и  , то существует такая взаимно однозначная функция , то существует такая взаимно однозначная функция 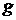 с множеством значений с множеством значений  , что , что  . .
Д о к а з а т е л ь с т в о. Пусть  . Если . Если  , то , то 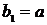 и функция и функция  взаимно однозначно отображает взаимно однозначно отображает  на на  , поэтому достаточно взять , поэтому достаточно взять  . Если . Если  , то , то  и аналогично и аналогично  . Легко проверить, что функция . Легко проверить, что функция 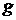 , заданная равенствами , заданная равенствами  , если , если  и и  удовлетворяет лемме. удовлетворяет лемме.
Теорема 2. Пусть 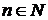 . Следующие условия эквивалентны: . Следующие условия эквивалентны:
I. 
II. Существуют множества 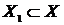 и элемент и элемент  , для которых , для которых  и и  . .
III.  и, если для множества и, если для множества 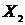 и элементы и элементы  , не принадлежащие ему, , не принадлежащие ему, 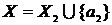 , то , то  . .
Д о к а з а т е л ь с т в о.
 . Пусть . Пусть 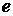 - последовательность с - последовательность с 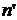 попарно различными членами и множеством значений попарно различными членами и множеством значений  . Взяв . Взяв  и и  , получим условие II. , получим условие II.
 . Условие . Условие  непосредственно следует из II. Обозначим через непосредственно следует из II. Обозначим через  и и  множество и элемент, удовлетворяющие условию II. Тогда множество и элемент, удовлетворяющие условию II. Тогда  и, значит, существует взаимно однозначная функция, отображающая и, значит, существует взаимно однозначная функция, отображающая  на на  . .
Согласно лемме, существует функция 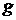 , взаимно однозначно отображающая , взаимно однозначно отображающая  на на 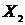 ; следовательно, ; следовательно,  в силу теоремы 1. в силу теоремы 1.
 . Пусть . Пусть 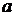 - произвольный элемент множества - произвольный элемент множества  и и  . Согласно условию III, . Согласно условию III,  и, значит, и, значит,  - множество значений некоторой последовательности - множество значений некоторой последовательности 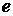 с с  попарно различными членами. Последовательность попарно различными членами. Последовательность  с с 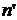 членами, заданная равенствами членами, заданная равенствами  для для  , ,  , имеет попарно различные члены, а множеством значений её является , имеет попарно различные члены, а множеством значений её является  . Следовательно . Следовательно  . .
Теорема 3. Если  , ,  , то , то 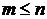 тогда и только тогда, когда существует такое множество тогда и только тогда, когда существует такое множество  , что , что  является его взаимно однозначным образом. является его взаимно однозначным образом.
Д о к а з а т е л ь с т в о. Если 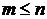 , то , то  . Пусть . Пусть  - множество значений последовательности - множество значений последовательности 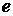 с с  попарно различными членами, а попарно различными членами, а  - множество значений последовательности - множество значений последовательности  с с 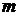 попарно различными членами. Тогда функция попарно различными членами. Тогда функция  взаимно однозначна и отображает взаимно однозначна и отображает  на некоторые подмножества множества на некоторые подмножества множества  (т.е. (т.е.  ). ).
Обратно, предположим, что существуют множество  и взаимно однозначная функция и взаимно однозначная функция  , отображающая , отображающая 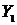 на на  . .
Доказательство проведём индукцией по  . Если . Если 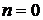 , то , то  , поэтому , поэтому 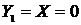 и, значит, и, значит,  и и 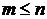 . Пусть . Пусть 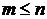 для некоторого для некоторого 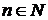 , и пусть , и пусть 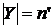 . Тогда . Тогда  , где , где  и и  . Т.к. . Т.к.  , то , то  . .
Множество  или 1) пусть, или 2) равно или 1) пусть, или 2) равно 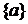 . .
В 1-м случае будет  . Тогда поскольку . Тогда поскольку  , ,  , можно применить индукцию и получить , можно применить индукцию и получить 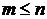 , а значит, , а значит,  . .
Во 2-м случае в силу теоремы 2  , где , где  . По предположению индукции . По предположению индукции  , откуда , откуда 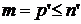 , и теорема доказана. , и теорема доказана.
Теорема 4. Если  , ,  и и 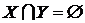 , то , то  . .
Д о к а з а т е л ь с т в о. Проведем индукцией по  . .
1) Для 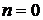  и, значит, теорема верна. и, значит, теорема верна.
2) Пусть теорема верна для некоторого числа  , и пусть , и пусть 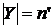 . Тогда . Тогда 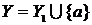 , где , где  , и потому , и потому  , где , где  . По предположению индукции тогда . По предположению индукции тогда 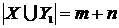 . Из Теоремы 2 следует, что . Из Теоремы 2 следует, что 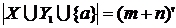 . Т.к. по определению суммы . Т.к. по определению суммы  , то теорема доказана. , то теорема доказана.
Следствие 5. Семейство всех конечных подмножеств произвольного множества  образует идеал (см. (II) §5, гл.I). образует идеал (см. (II) §5, гл.I).
Действительно, подмножество конечного множества конечно по теореме 3, а сумма конечных множеств конечна по теореме 3 и теореме 4.
Теорема 6. Если  , ,  , то множеств , то множеств  является взаимно однозначным образом множества является взаимно однозначным образом множества  и только тогда, когда и только тогда, когда 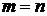 . .
Д о к а з а т е л ь с т в о. Если 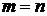 , то очевидно, что , то очевидно, что  - взаимно однозначный образ множества - взаимно однозначный образ множества  , т.к. существуют последовательности с , т.к. существуют последовательности с  попарно различными членами, отображающие множество попарно различными членами, отображающие множество  соответственно на соответственно на  и и  . .
Обратно, пусть  - взаимно однозначный образ множества - взаимно однозначный образ множества  . Тогда . Тогда 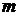 - взаимно однозначный образ множества - взаимно однозначный образ множества  . Докажем по индукции, что . Докажем по индукции, что 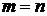 . .
1) Для 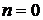 теорема верна (очевидно). теорема верна (очевидно).
2) Пусть теорема верна для некоторого  , и пусть , и пусть 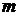 - взаимно однозначный образ множества - взаимно однозначный образ множества 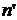 . Поскольку . Поскольку  , положим , положим  . Т.к. . Т.к.  и и  , то, согласно лемме (между теоремой 1 и теоремой 2 настоящего параграфа), , то, согласно лемме (между теоремой 1 и теоремой 2 настоящего параграфа),  является взаимно однозначным образом множества является взаимно однозначным образом множества  и, значит, согласно предположению индукции, и, значит, согласно предположению индукции,  , откуда , откуда  , и теорема доказана. , и теорема доказана.
Следствие 7 (Принцип Дирихле). Если  , ,  , ,  , то функция , то функция  , для которой , для которой 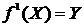 , не взаимно однозначна. , не взаимно однозначна.
Сам Дирихле содержательно сформулировал этот принцип так:
Если 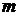 предметов разместить в предметов разместить в  ящиках, ящиках,  , то хотя бы один ящик будет содержать не менее двух предметов. , то хотя бы один ящик будет содержать не менее двух предметов.
Очевидно, что наша функция  и есть как раз та функция, которая ставит в соответствие каждому предмету ящик, в который помещен этот предмет. Из доказанных теорем выведем теперь следствия для бесконечных множеств. и есть как раз та функция, которая ставит в соответствие каждому предмету ящик, в который помещен этот предмет. Из доказанных теорем выведем теперь следствия для бесконечных множеств.
Теорема 8. Если  бесконечно и бесконечно и  , то и , то и  бесконечно. бесконечно.
Это следует непосредственно из теоремы 3.
Теорема 9. Если  бесконечно, а бесконечно, а  конечно, то разность конечно, то разность  бесконечна. бесконечна.
Это следует из теоремы 4.
Теорема 10. Множество 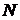 бесконечно. бесконечно.
Д о к а з а т е л ь с т в о. Докажем методов от противного. Предположим, что  , где , где 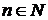 . Т.к. . Т.к.  , то в силу теоремы 3 множество , то в силу теоремы 3 множество 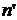 имеет имеет 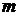 элементов, где элементов, где 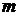 - такой элемент множества - такой элемент множества 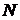 , что , что 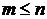 . Т.к. . Т.к.  для каждого для каждого  , то , то  , что приводит к противоречию выражению 4 (§1, гл.III). , что приводит к противоречию выражению 4 (§1, гл.III).
|


 имеет
имеет  элементов
элементов  , и пишут
, и пишут  , если существует последовательность с
, если существует последовательность с  ; в противном случае оно называется бесконечным.
; в противном случае оно называется бесконечным. , т.к. единственной последовательностью с 0 членами является пустая последовательность.
, т.к. единственной последовательностью с 0 членами является пустая последовательность. множество
множество  имеет
имеет  , является, согласно определению последовательности, последовательностью с
, является, согласно определению последовательности, последовательностью с  взаимно однозначно отображает множество
взаимно однозначно отображает множество  , то условия
, то условия  эквивалентны.
эквивалентны.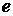 - последовательность с
- последовательность с  - последовательность с
- последовательность с 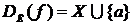 ,
, 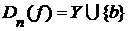 и
и  , то существует такая взаимно однозначная функция
, то существует такая взаимно однозначная функция 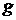 с множеством значений
с множеством значений  .
. . Если
. Если  , то
, то 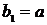 и функция
и функция  . Если
. Если  , то
, то  и аналогично
и аналогично  . Легко проверить, что функция
. Легко проверить, что функция  , если
, если  и
и  удовлетворяет лемме.
удовлетворяет лемме.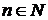 . Следующие условия эквивалентны:
. Следующие условия эквивалентны:
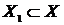 и элемент
и элемент  , для которых
, для которых  и
и  .
. и, если для множества
и, если для множества 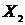 и элементы
и элементы  , не принадлежащие ему,
, не принадлежащие ему, 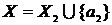 , то
, то  .
. . Пусть
. Пусть 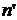 попарно различными членами и множеством значений
попарно различными членами и множеством значений  и
и  , получим условие II.
, получим условие II. . Условие
. Условие  и
и  множество и элемент, удовлетворяющие условию II. Тогда
множество и элемент, удовлетворяющие условию II. Тогда  и, значит, существует взаимно однозначная функция, отображающая
и, значит, существует взаимно однозначная функция, отображающая  на
на  .
. . Пусть
. Пусть 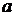 - произвольный элемент множества
- произвольный элемент множества  с
с  для
для  ,
,  , имеет попарно различные члены, а множеством значений её является
, имеет попарно различные члены, а множеством значений её является  ,
, 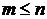 тогда и только тогда, когда существует такое множество
тогда и только тогда, когда существует такое множество  , что
, что  . Пусть
. Пусть 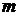 попарно различными членами. Тогда функция
попарно различными членами. Тогда функция  взаимно однозначна и отображает
взаимно однозначна и отображает  ).
).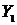 на
на 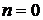 , то
, то  , поэтому
, поэтому 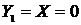 и, значит,
и, значит,  и
и 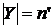 . Тогда
. Тогда  , где
, где  и
и  . Т.к.
. Т.к.  , то
, то  .
. или 1) пусть, или 2) равно
или 1) пусть, или 2) равно 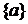 .
. . Тогда поскольку
. Тогда поскольку  ,
,  , можно применить индукцию и получить
, можно применить индукцию и получить  .
. , где
, где  . По предположению индукции
. По предположению индукции  , откуда
, откуда 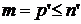 , и теорема доказана.
, и теорема доказана.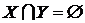 , то
, то  .
.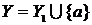 , где
, где  , и потому
, и потому  , где
, где  . По предположению индукции тогда
. По предположению индукции тогда 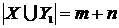 . Из Теоремы 2 следует, что
. Из Теоремы 2 следует, что 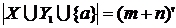 . Т.к. по определению суммы
. Т.к. по определению суммы  , то теорема доказана.
, то теорема доказана. образует идеал (см. (II) §5, гл.I).
образует идеал (см. (II) §5, гл.I).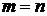 .
. , положим
, положим  и
и  , то, согласно лемме (между теоремой 1 и теоремой 2 настоящего параграфа),
, то, согласно лемме (между теоремой 1 и теоремой 2 настоящего параграфа),  , откуда
, откуда  , и теорема доказана.
, и теорема доказана. , то функция
, то функция 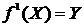 , не взаимно однозначна.
, не взаимно однозначна. , то и
, то и  бесконечна.
бесконечна.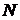 бесконечно.
бесконечно. , где
, где  , то в силу теоремы 3 множество
, то в силу теоремы 3 множество  для каждого
для каждого  , что приводит к противоречию выражению 4 (§1, гл.III).
, что приводит к противоречию выражению 4 (§1, гл.III).