
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
А затем упорядочить из в последовательность Пара Примечание.
В частности
2. Отображение множества Определим по индукции последовательность взаимно однозначных функций так, чтобы
Теорема 3. Функция Д о к а з а т е л ь с т в о. Для
Осталось доказать, что для каждого По предположению индукции существует такая последовательность 3. Отображение множества всех конечных последовательностей натуральных чисел на Обозначим для
Эта функция взаимно однозначно отображает множество всех непустых конечных последовательностей натуральных чисел на множество Теорема 4. Существует функция  Достаточно для непустых последовательностей 4. Отображение множества Пусть
Таким образом, если Аналогичные определения принимаем и для бесконечных последовательностей натуральных чисел. Пусть
Таким образом, Теорема 5. Сужение функции Теорема 6. Для любого Доказать самостоятельно. 5. Отображение множества Положим для
т.е. Теорема 7. Функция Д о к а з а т е л ь с т в о. Очевидно, что
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 250. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
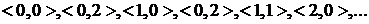 (4)
(4)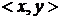 стоит в этой последовательности на месте
стоит в этой последовательности на месте 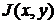 . Пара, стоящая на месте
. Пара, стоящая на месте 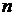 , встречается в таблице (3) в строке с номерами
, встречается в таблице (3) в строке с номерами 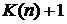 и столбце с номером
и столбце с номером 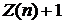 .
.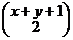 - биноминальный коэффициент (см. Т. и Г. Корн “Справочник по математике” стр. 638).
- биноминальный коэффициент (см. Т. и Г. Корн “Справочник по математике” стр. 638).
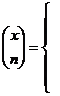
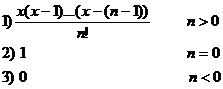

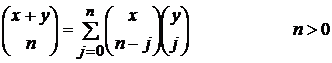
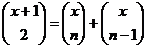
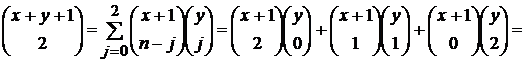
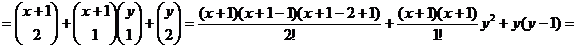
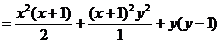 .
.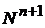 на
на 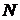 .
.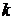 -я функция в этой последовательности, обозначается
-я функция в этой последовательности, обозначается 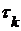 , взаимно однозначно отображала множество
, взаимно однозначно отображала множество 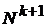 на
на 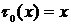 для
для 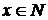
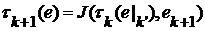 для
для 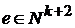
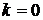 теорема очевидна. Предположим, что она верна для
теорема очевидна. Предположим, что она верна для 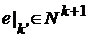 , откуда
, откуда 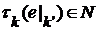 и по определению
и по определению 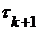 отображает
отображает 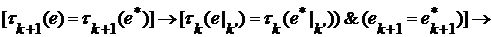
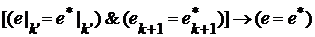 .
.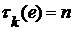 .
.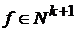 , что
, что 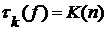 . Искомой последовательностью
. Искомой последовательностью 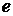 будет последовательность, у которой первые
будет последовательность, у которой первые 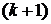 члены совпадают с
члены совпадают с  , а последним членом является
, а последним членом является 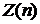 . Действительно, для такой последовательности
. Действительно, для такой последовательности 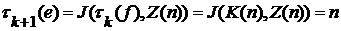 .
.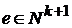
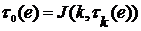 .
.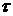 , отображающая взаимно однозначно множество
, отображающая взаимно однозначно множество 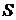 всех конечных последовательностей натуральных чисел на множество
всех конечных последовательностей натуральных чисел на множество 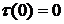 .
.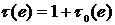 и
и 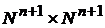 на
на 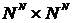 на
на 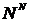 .
.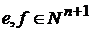 :
: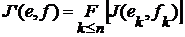 ,
, 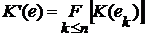 ,
, 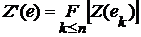 .
.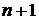 с членами
с членами 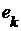 и
и 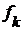 соответственно,
соответственно, 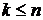 , то
, то 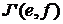 - последовательность длины
- последовательность длины 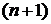 с членами
с членами 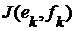 ,
, 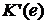 и
и 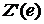 - последовательности с членами
- последовательности с членами 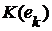 и
и 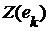 ,
,  . Положим
. Положим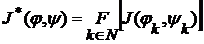 ,
, 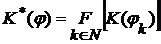 ,
, 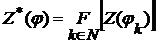 .
.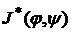 - бесконечная последовательность, у которой
- бесконечная последовательность, у которой 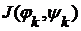 , а
, а 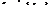 и
и 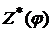 - бесконечные последовательности,
- бесконечные последовательности, 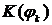 и
и 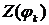 .
.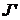 на множество
на множество 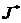 взаимно однозначно отображает множество
взаимно однозначно отображает множество 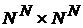 на
на 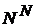 .
.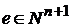 и любого
и любого 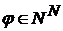 имеют место равенства
имеют место равенства 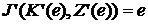 ,
, 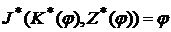 .
. 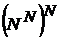 .
.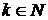 и
и 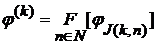 ,
,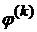 - последовательность
- последовательность 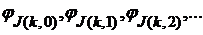
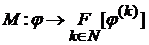 (ставящая в соответствие последовательности
(ставящая в соответствие последовательности 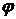 последовательность
последовательность 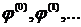 ) взаимно однозначно отображает множество
) взаимно однозначно отображает множество 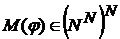 для каждого
для каждого 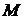 взаимно однозначна, т.к. из равенства
взаимно однозначна, т.к. из равенства 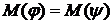 следует, что
следует, что 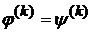 для каждого натурального
для каждого натурального 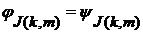 для любых
для любых 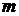 . В частности, для
. В частности, для 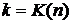 и
и 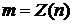 имеем
имеем 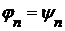 для всех
для всех  , членами
, членами 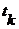 которой являются элементы множества
которой являются элементы множества 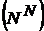 (
( 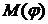 при надлежащем выборе
при надлежащем выборе 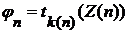 , то
, то 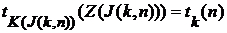 , т.е.
, т.е. 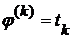 для всех
для всех 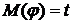 .
.