
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Множество K будем называть индуктивным, если для него выполняются равенства (I) и (II).Стр 1 из 24Следующая ⇒ ГЛАВА III. НАТУРАЛЬНЫЕ ЧИСЛА. КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ МНОЖЕСТВА. В этой главе мы исходим из системы аксиом ∑º, причём, как обычно теоремы, не помеченные символом º, можно доказать без аксиомы выбора VI.
Натуральные числа. Для каждого множества X обозначим
Множество X' называется последователем множества X. Теорема 1. Существует единое семейство K множеств N, обладающие следующими свойствами: I. II. III. Если K удовлетворяет I и II, то Множество K будем называть индуктивным, если для него выполняются равенства (I) и (II). Д о к а з а т е л ь с т в о.Из аксиомы бесконечности (IV) следует, что существует по крайней мере одно семейство R, обладающее свойствами (I) и (II). Пусть Ф – семейство всех тех подмножеств семейства R, которые обладают свойствами (I) и (II):
Легко проверить, что P(Ф) является искомым семейством K. Элементами множества N будут множества 0, {0}, {0, {0}}, … Можно считать, что эти множества играют роль натуральных чисел 0, 1, 2, 3,.. , а роль операции +1 играет операция '. Мы докажем теоремы, из которых будет следовать, что для элементов множества N выполняются известные законы арифметики. Для упрощения символики будем в дальнейшем обозначать элементы семейства N буквами m, n, p, … Прежде всего докажем, что Пусть Чтобы доказать (II), возьмём Доказательства такого вида называют доказательствами по индукции.  Далее Доказательство (2) проводится по индукции; оно основано на том, что множество В самом деле, Пеано показал, что арифметику натуральных чисел можно построить, исходя из следующих аксиом: a) нуль является натуральным числом; b) каждое натуральное число имеет последовательность; c) нуль не является последователем никакого натурального числа; d) числа, имеющие одинаковые последователи, равны; e) множество, содержащее нуль и вместе с каждым число его последователь, содержит все натуральные числа. Из формул (I), (II), (3), (III) и Для произвольных m, n выполняется одна и только одна из (4) зависимостей Д о к а з а т е л ь с т в о. Из (1) и (2) следует, что любые две из этих зависимостей исключают друг друга. Чтобы доказать, что для каждой пары m, n одна из этих зависимостей выполняется, применим индукцию. Обозначим
Утверждение (4) равносильно утверждению Множество K(0) индуктивно, т.к. K(0) состоит из множества 0 и тех m, для которых Пусть K(n) индуктивно, т.е. Т.к. первые два члена этой дизъюнкции ложны, то Проверим условие (II). Пусть Во 2-м и 3-м случае очевидно, что В 1-м случае: · или · или поскольку по предположению множество Отсюда получаем Учитывая, что Множество Д о к а з а т е л ь с т в о. Множество Рассмотрим для этого множество Чтобы доказать, что Z удовлетворяет условию (II), возьмем элемент
1) 2) В 1-м случае В арифметике множество чисел, больших данного числа n, определяется как общая часть всех множеств, содержащих последовательность числа n и вместе с каждым числом b содержащих его последовательность. Утверждение (5) показывает, что отношение принадлежности в множестве Введение множества Функцию, определенную на множестве Очевидно, что множеством всех бесконечных последовательностей, члены которых принадлежат множеству A, будет AN; множеством всех конечных последовательностей с
Из этого определения следует, что такое множество существует.
Определения по индукции. Наиболее характерной особенностью арифметики натуральных чисел является возможность определять понятия с помощью индукции. Простейший случай представляет собой определение последовательности a) b) Это определение по индукции с параметром Схемы (a) и (b) соответствуют переходу от « В случае индукции с параметрами значение c) d) В схеме (c) В схеме (d) Примеры определения по индукции. Пример 1. Функция сложения
Это определение попадает под схему (b), где Пример 2. Функция
Это определение попадает под схему (a), где Пример 3. Пусть в схеме (b) Функцию Таким образом, Пример 4. Пусть Тогда Функция Очевидно, что схема (d) наиболее общая из всех упомянутых здесь схем. Это означает, что при подходящем выборе функций
Покажем теперь, что схему (d) в свою очередь можно свести к схеме (a). Пусть Очевидно, что
Связь между
причём
Отсюда видно, что последовательность
Теперь докажем существование и единственность функции, удовлетворяющей равенствам (a). Такая теория позволяет нам пользоваться определениями по индукции по схеме (a). Согласно сделанному выше замечанию, отсюда будет следовать существование функций, удовлетворяющих равенствам (b), (c), (d). Единственность этих функций доказывается так же, как и для схемы (a), и в дальнейшем мы будем пользоваться определениями по индукции по любой из схем (a)-(d). Теорема 1. Если Д о к а з а т е л ь с т в о. Единственность. Пусть равенствам (a) удовлетворяют две последовательности Существование. Пусть
Другими словами, Докажем по индукции, что существует единственная функция В качестве Т.к. Если Часто определяются по индукции не одна, а одновременно несколько функций (со значениями из одного и того же множества
где Такое определение также сводится к предыдущим определениями. Достаточно заметить, что для последовательности Справедливы формулы:
где Таким образом, функция
Теорема 2. Для любого множества Д о к а з а т е л ь с т в о. Единственность доказывается так же, как в теореме 1. Для доказательства существования
Как и в теореме 1, легко показать, что существует единственная функция Из единственности функции Пример. Пусть
§3. Отображение множества N Определение по индукции несколько важных отображений, которыми в дальнейшем будет часто пользоваться. 1. Отображение множества Положим для
Теорема 1. Функция Д о к а з а т е л ь с т в о. Пусть Откуда следовало бы, что
Но это невозможно, т.к.
Аналогично доказывается, что не может быть
Предположение
Аналогично сведем к противоречию предположение Покажем теперь, что множество Если Если Теорема 2. Существуют функции Д о к а з а т е л ь с т в о. Существование функций Замечание. Индуктивность функций Nстолбца=Z(n)+1 Nстроки |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 310. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
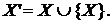
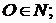
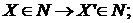

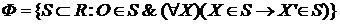
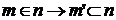 (1)
(1)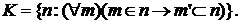 Достаточно показать, что
Достаточно показать, что 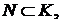 т.е. что множество K индуктивно. Условие (I) выполняется очевидно.
т.е. что множество K индуктивно. Условие (I) выполняется очевидно.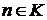 и
и 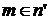 . Тогда
. Тогда 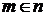 или
или 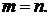 В 1-ом случае
В 1-ом случае 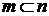 по определению множества K, а во 2-ом случае
по определению множества K, а во 2-ом случае 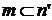 , значит,
, значит, 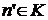 и формула (1) доказана.
и формула (1) доказана.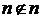 (2).
(2).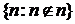 индуктивно
индуктивно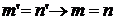 (3)
(3)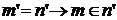 и значит,
и значит, 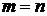 , откуда согласно (1),
, откуда согласно (1), 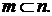 Аналогично доказывается обратное включение.
Аналогично доказывается обратное включение.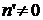 следует, что элементы множества N удовлетворяют всем аксиомам Пеано.
следует, что элементы множества N удовлетворяют всем аксиомам Пеано.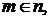
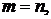
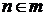 .
.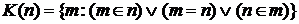
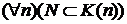 , поэтому достаточно показать, что множество K(n) для любого n индуктивно.
, поэтому достаточно показать, что множество K(n) для любого n индуктивно.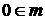 и
и 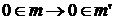 .
.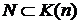 . Покажем, что K(n') также индуктивно. Из
. Покажем, что K(n') также индуктивно. Из 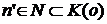 следует, что
следует, что 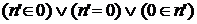 .
.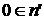 , следовательно,
, следовательно, 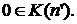 Условие (I) индуктивности множества выполнено.
Условие (I) индуктивности множества выполнено.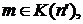 т.е. выполняется один из случаев
т.е. выполняется один из случаев 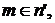
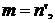
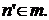
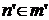 и, значит,
и, значит, 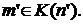
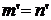 и, значит,
и, значит, 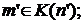
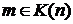 и
и 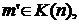
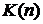 индуктивно.
индуктивно.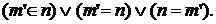 3-й член этой дизъюнкции можно отбросить, т.к. он вместе с
3-й член этой дизъюнкции можно отбросить, т.к. он вместе с 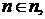 что противоречит (2). Таким образом, остаются только возможности
что противоречит (2). Таким образом, остаются только возможности 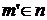 и
и 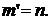
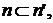 получаем в обоих случаях
получаем в обоих случаях 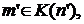 и утверждение (4) доказано.
и утверждение (4) доказано.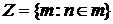 совпадает с произведением
совпадает с произведением 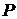 всех семейств
всех семейств 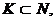 удовлетворяющих условию (II) и содержащих
удовлетворяющих условию (II) и содержащих 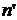 . (5)
. (5)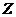 удовлетворяет условию (II), т.к.
удовлетворяет условию (II), т.к. 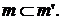 Из этого следует, что
Из этого следует, что 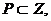 поскольку
поскольку 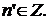 Остаётся показать, что если K удовлетворяет условию (II) и
Остаётся показать, что если K удовлетворяет условию (II) и 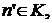 то
то 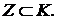
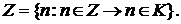 Достаточно показать, что
Достаточно показать, что 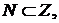 т.е. что Z индуктивно. Условие (I) с очевидностью выполняется, т.к.
т.е. что Z индуктивно. Условие (I) с очевидностью выполняется, т.к. 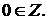
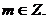
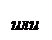 Тогда:
Тогда: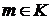
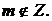
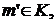 поскольку
поскольку 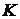 удовлетворяет условию (II) и, значит,
удовлетворяет условию (II) и, значит, 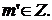 2-й случай, согласно (4), распадается на 3 подслучая в соответствии с зависимостями
2-й случай, согласно (4), распадается на 3 подслучая в соответствии с зависимостями 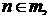
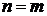 и
и 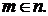 1-й подслучай противоречит условию
1-й подслучай противоречит условию 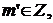 т.к.
т.к. 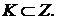 Наконец, в последнем случае, согласно (4),
Наконец, в последнем случае, согласно (4), 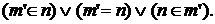 Если верны 1-й и 2-й члены этой дизъюнкции, то опять же по (4)
Если верны 1-й и 2-й члены этой дизъюнкции, то опять же по (4) 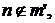 поэтому
поэтому 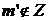 и
и 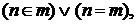 в то время как по условию
в то время как по условию 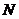 соответствует отношению «меньше» между натуральными числами. Поэтому вместо
соответствует отношению «меньше» между натуральными числами. Поэтому вместо 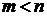 и
и 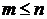 соответственно.
соответственно.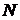 даёт возможность определить в теории множеств понятия, аналогичные понятиям арифметики и анализа. Например, функция
даёт возможность определить в теории множеств понятия, аналогичные понятиям арифметики и анализа. Например, функция 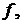 определенная на множестве
определенная на множестве 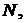 называется бесконечной последовательностью и иногда обозначается
называется бесконечной последовательностью и иногда обозначается 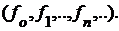
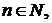 называют конечной последовательностью с
называют конечной последовательностью с 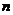 членами.
членами. членами будет AN. Множество всех конечных последовательностей с членами из A можно определить так:
членами будет AN. Множество всех конечных последовательностей с членами из A можно определить так: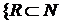 ×
× 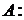 (R – функция)
(R – функция) 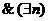
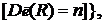
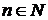
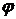 (члены которой принадлежат некоторому множеству
(члены которой принадлежат некоторому множеству 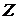 ), удовлетворяющий равенствам:
), удовлетворяющий равенствам: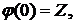
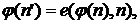 где
где 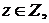 а
а 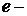 функция, отображающая
функция, отображающая 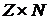 в
в 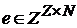 ).
).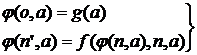
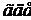
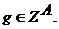
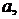 пробегающим множество
пробегающим множество 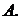
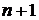 », т.е. значение
», т.е. значение 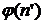 (или
(или 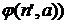 зависит от значения
зависит от значения 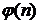 (или
(или 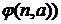 . Значение
. Значение 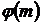 , где
, где 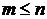 (т.е.
(т.е. 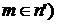 .
.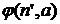 может зависеть от всех значений
может зависеть от всех значений 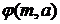 , где
, где 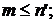 или даже от всех значений
или даже от всех значений 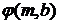 , где
, где 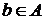 и
и 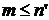 . Таким образом, мы приходим к следующим схемам определения его индукции:
. Таким образом, мы приходим к следующим схемам определения его индукции: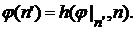
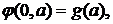
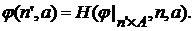
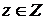 и
и 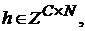 где
где 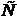 - множество конечных последовательностей с членами из
- множество конечных последовательностей с членами из 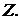
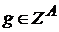 и
и 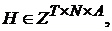 где
где 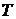 - множество функций со значениями в
- множество функций со значениями в 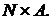
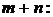
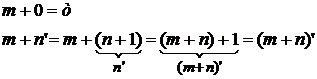
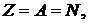
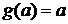 и
и 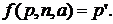
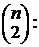
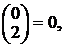
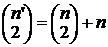
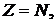
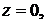
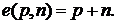
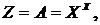
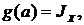
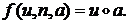 Тогда
Тогда 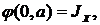
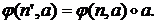
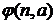 будет обозначать
будет обозначать 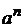 и называть
и называть 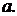 (Итерация – повторное (
(Итерация – повторное ( 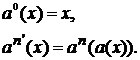
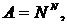 и пусть в схеме (b):
и пусть в схеме (b):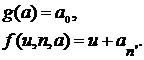
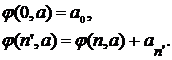
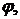 определённая по такой схеме, обозначается
определённая по такой схеме, обозначается  Аналогично определяется
Аналогично определяется 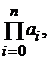
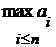 и т.п.
и т.п.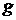 и
и 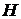 можно получить из (d) любую из схем (a), (b), (c). Например, возьмём в качестве
можно получить из (d) любую из схем (a), (b), (c). Например, возьмём в качестве 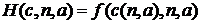 для
для 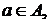
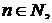
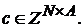 Получим из (d) схему (b).
Получим из (d) схему (b).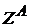 и
и 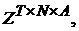 и пусть
и пусть 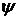 , заданную формулой
, заданную формулой 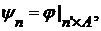 можно определить по схеме (a).
можно определить по схеме (a).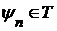 для каждого
для каждого 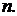 Первый член последовательности
Первый член последовательности 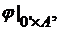 т.е. множеству:
т.е. множеству: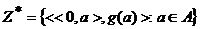 .
.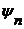 и
и 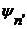 задаётся формулой:
задаётся формулой: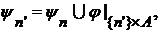
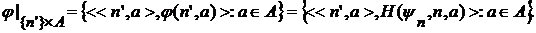
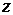 множеством
множеством 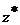 и полагая
и полагая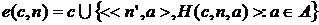 для
для 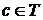
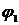 и
и 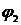 . Рассмотрим множество
. Рассмотрим множество 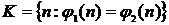 . Из (a) следует, что множество K индуктивно, поэтому
. Из (a) следует, что множество K индуктивно, поэтому 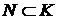 и
и 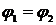 .
.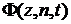 - высказывательная функция
- высказывательная функция 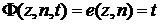 , a
, a 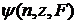 - высказывательная функция вида:
- высказывательная функция вида: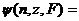 (F есть функция)&
(F есть функция)& 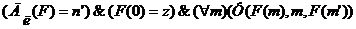
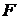 -функция, определённая на множестве чисел
-функция, определённая на множестве чисел 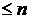 , для которой
, для которой 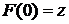 и
и 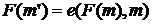 для всех
для всех 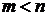 .
.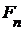 , удовлетворяющая
, удовлетворяющая 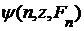 . Единственность доказывается так же, как единственность последовательности
. Единственность доказывается так же, как единственность последовательности 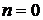 достаточно взять в качестве
достаточно взять в качестве 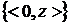 . Если
. Если 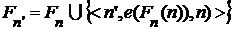 удовлетворяет
удовлетворяет 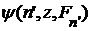 .
.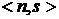 , что
, что 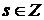 и
и 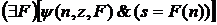 .
.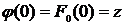 .
.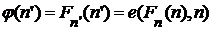 , по определению функции
, по определению функции 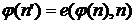 .
.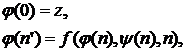
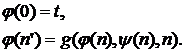
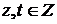 ;
; 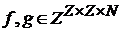 .
.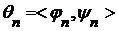 .
.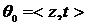 ,
, 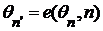 ,
,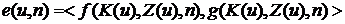 , а
, а 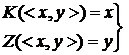 для
для 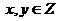 .
.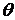 определена индуктивно по схеме (a). Определим теперь функции
определена индуктивно по схеме (a). Определим теперь функции 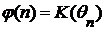 ,
, 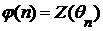 . Теорему об определениях по индукции можно обобщить на случай операций. Ограничится только одним частным случаем. Пусть
. Теорему об определениях по индукции можно обобщить на случай операций. Ограничится только одним частным случаем. Пусть 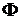 - такая высказывательная функция, что
- такая высказывательная функция, что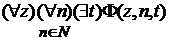 ,
,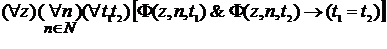 .
. существует одна и только одна такая последовательность
существует одна и только одна такая последовательность  и
и 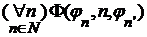 .
.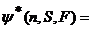 (F есть функция)
(F есть функция) 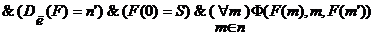
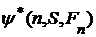 . Чтобы и дальше следовать схеме доказательства теоремы 1, мы должны быть уверены, что существует множество, содержащее все элементы вида
. Чтобы и дальше следовать схеме доказательства теоремы 1, мы должны быть уверены, что существует множество, содержащее все элементы вида 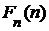 , где
, где 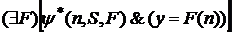 удовлетворяет условиям аксиомы VII. Поэтому, согласно аксиоме VII, существует образ множества
удовлетворяет условиям аксиомы VII. Поэтому, согласно аксиоме VII, существует образ множества 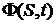 - высказывательная функция
- высказывательная функция 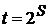 . Для произвольного множества
. Для произвольного множества 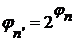 для каждого натурального
для каждого натурального 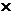 N на N и связанные с ним отображения.
N на N и связанные с ним отображения.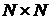 на
на 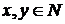 .
.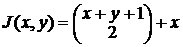 .
.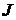 взаимно однозначно отображает множество
взаимно однозначно отображает множество 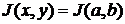 . Покажем сначала, что
. Покажем сначала, что 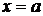 . Если бы было
. Если бы было 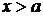 , т.е.
, т.е. 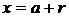 ,
, 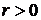 , то мы имели бы
, то мы имели бы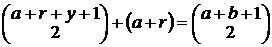 (1)
(1)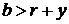 , т.к.
, т.к. 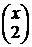 - возрастающая функция. Значит,
- возрастающая функция. Значит, 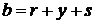 , где
, где 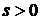 . Подставив в (1) и обозначив
. Подставив в (1) и обозначив 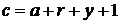 , мы получили бы
, мы получили бы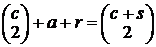
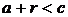 , и, значит,
, и, значит,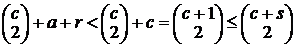
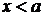 . Значит,
. Значит, 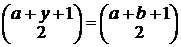
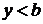 , т.е.
, т.е. 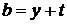 ,
, 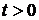 , ведет к противоречию
, ведет к противоречию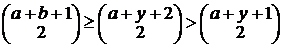
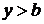 . Итак, взаимная однозначность функции
. Итак, взаимная однозначность функции 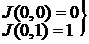 следует, что
следует, что 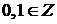 . Пусть
. Пусть 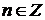 . Это значит, что существует
. Это значит, что существует 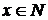 и
и 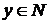 , для которых
, для которых 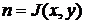 .
.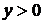 , то
, то 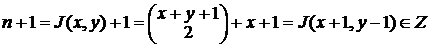 .
.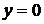 , то
, то 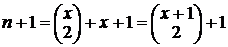 . Для
. Для 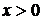 это выражение можно переписать в виде
это выражение можно переписать в виде 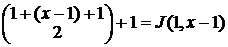 . И, значит, снова
. И, значит, снова 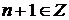 . Наконец, если
. Наконец, если 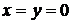 , то
, то 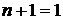 , так что и здесь
, так что и здесь 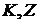 , отображающие
, отображающие 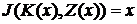 . Эти функции удовлетворяют неравенствам
. Эти функции удовлетворяют неравенствам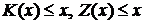 (2)
(2)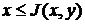 ,
, 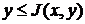 .
.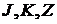 становится ясным, если расположить пары
становится ясным, если расположить пары 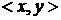 натуральных чисел в бесконечную таблицу
натуральных чисел в бесконечную таблицу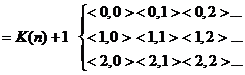 (3)
(3)