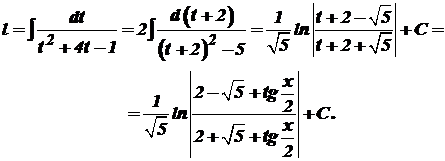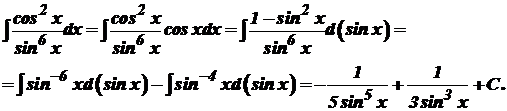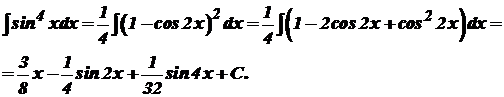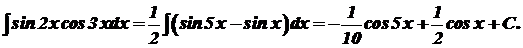Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Інтегрування деяких тригонометричних функцій⇐ ПредыдущаяСтр 14 из 14 Розглянемо деякі типи інтегралів від тригонометричних функцій, які обчислюються в скінченному вигляді. До них належать інтеграли від раціональних функцій відносно функцій де Інтеграли такого виду можна звести до інтегралів від раціональної функції за допомогою так званої універсальної тригонометричної підстановки Справді,
Крім того, Інтеграл (33) після заміни змінної (34) набуває вигляду
Таким чином, інтеграл виду (33) завдяки підстановці (34) завжди можна обчислити в скінченому вигляді. Однак застосування підстановки (34) не завжди доцільне. В окремих випадках можна використати інші, простіші методи. Це стосується, зокрема, інтегралів виду де Для обчислення інтеграла (35) застосуємо підстановку
Матимемо
Отже, де Аналогічно, якщо скористатися підстановкою  то інтеграл (36) набуває вигляду де При обчисленні інтегралів від тригонометричних функцій часто доводиться користуватися відомими формулами тригонометрії. Розглянемо інтеграли Для знаходження цих інтегралів застосовують такі формули: Якщо Аналогічно обчислюють і два інші інтеграли. При
Якщо Зауважимо, що метод обчислення інтегралів (40) і (42) використовується і для інтегралів виду
Приклади
Знайти інтеграли: 1) Розв‘язання 1) Застосуємо підстановку Тоді
Маємо 2)
3)
4)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 394. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
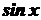 ,
, 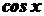 ,
, 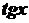 ,
, 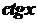 ,
, 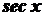 ,
, 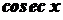 . Оскільки функції
. Оскільки функції 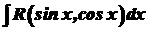 , (33)
, (33)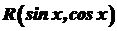 – раціональна функція від
– раціональна функція від 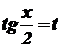 .
.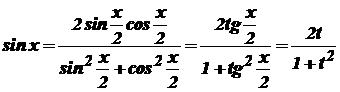 ;
;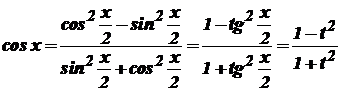 .
.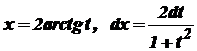 .
.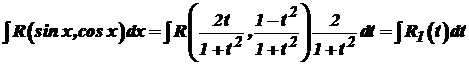 , де
, де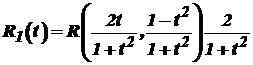 – раціональна функція від змінної
– раціональна функція від змінної 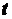 .
. ; (35)
; (35) , (36)
, (36) – ціле число;
– ціле число;  та
та 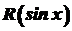 – раціональні функції від своїх аргументів.
– раціональні функції від своїх аргументів.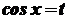 . (37)
. (37)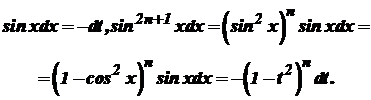
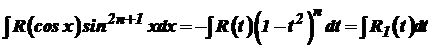 ,
, 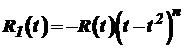 – раціональна функція від
– раціональна функція від 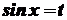 ,
,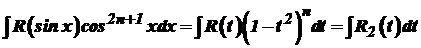 ,
,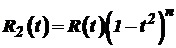 – раціональна функція від
– раціональна функція від 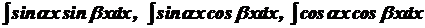 . (39)
. (39)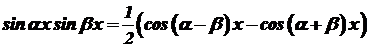 ;
;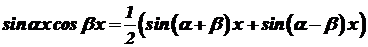 ;
;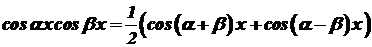 .
.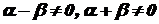 , то перший з інтегралів (39) обчислюють так:
, то перший з інтегралів (39) обчислюють так: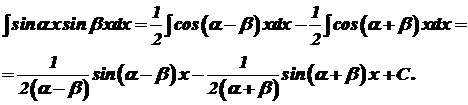
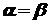 інтеграли (39) обчислюють так:
інтеграли (39) обчислюють так: ; (40)
; (40)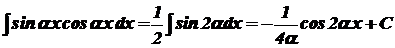 ; (41)
; (41)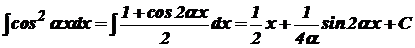 . (42)
. (42)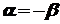 , то, використовуючи непарність функції
, то, використовуючи непарність функції 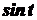 та парність функції
та парність функції 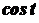 , знаходження інтегралів (39) зводиться до випадку
, знаходження інтегралів (39) зводиться до випадку 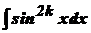 та
та 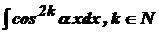 .
.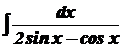 ; 2)
; 2) 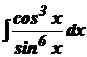 ; 3)
; 3) 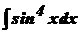 ; 4)
; 4) 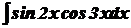 .
.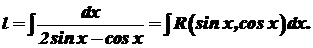
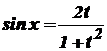 ,
, 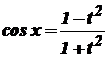 ,
, 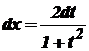 .
.