
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Похідні елементарних функцій Похідна сталої функції. Похідна функції Доведення.
Похідна степеневої функції
Зауваження. Якщо Приклади.
Похідна показникової функції
Приклади.
Похідна логарифмічної функції
Похідні тригонометричних функцій. Нехай
Аналогічно доводиться, що функція Якщо
Аналогічно доводиться, що функція
Похідна оберненої функції. Теорема. Нехай функція
Доведення. Надамо значенню
Якщо
Похідні обернених тригонометричних функцій. Нехай маємо функцію
Згідно теореми про похідну оберненої функції
Зауваження. Тут враховано, що при Аналогічно одержуються похідні інших обернених тригонометричних функцій: 
ЛЕКЦІЯ 17
13. Диференціал функції. 14. Похідні вищих порядків. 15. Формула Лейбніца для п-ної похідної добутку двох функцій. 16. Диференціали вищих порядків.
Диференціал функції Нехай функція
де Диференціалом функції Диференціал функції позначається так:
Враховуючи, що
Диференціалом незалежної змінної Отже,
Із останньої формули випливає, що похідну
Диференціал функції має наступний геометричний зміст. Нехай точка
Пряма Оскільки диференціал
Отже
Приклад. Знайти наближено Розв'язування. Розглянемо функцію Отже, Якщо функції
Нехай тепер маємо складену функцію
Так як
то
Оскільки Таким чином, якщо функція складена, то форма диференціалу не змінює свого виду. Цю властивість називають інваріантністю форми диференціалу.
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 457. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
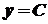 , де
, де 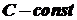 при
при 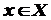 виражається формулою
виражається формулою 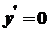 .
.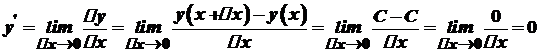 .
.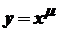 . Область визначення
. Область визначення 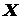 цієї функції залежить від
цієї функції залежить від 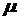 . Візьмемо довільну відмінну від нуля внутрішню точку
. Візьмемо довільну відмінну від нуля внутрішню точку 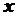 області визначення
області визначення 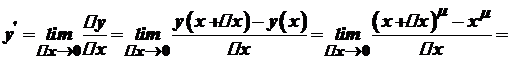
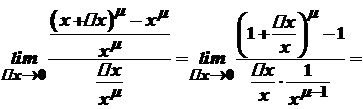
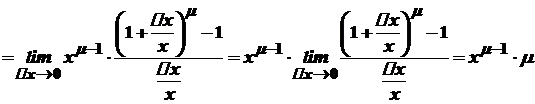 .
.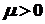 , то легко безпосередньо одержати значення похідної при
, то легко безпосередньо одержати значення похідної при 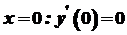 . Отже, для будь-якої точки
. Отже, для будь-якої точки 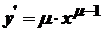 .
.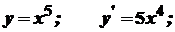
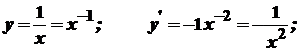
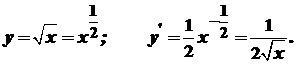
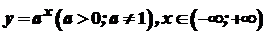 .
.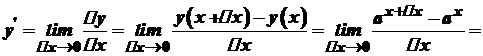
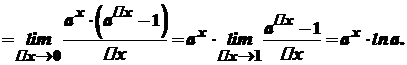
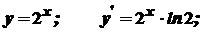
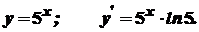
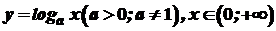 .
.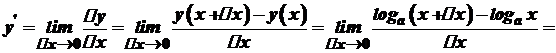
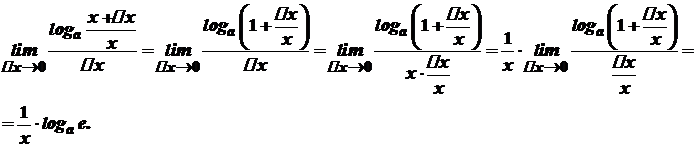 Зокрема, якщо
Зокрема, якщо 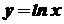 , то
, то 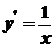 .
.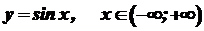 . Тоді
. Тоді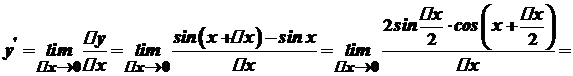
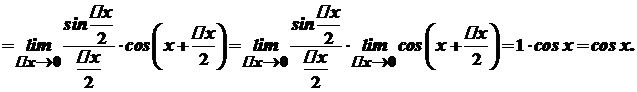
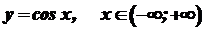 має похідну
має похідну 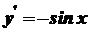 .
.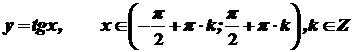 , то
, то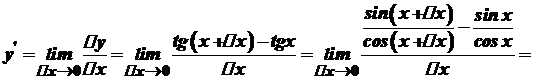
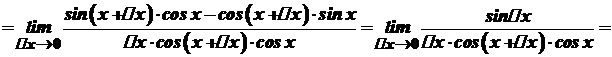
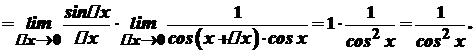
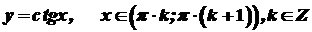 має похідну
має похідну 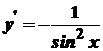 .
.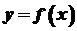 задовольняє всі умови теореми про існування оберненої функції і в точці
задовольняє всі умови теореми про існування оберненої функції і в точці 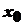 має похідну
має похідну  . Тоді обернена до неї функція
. Тоді обернена до неї функція 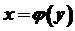 у точці
у точці 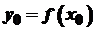 має похідну і
має похідну і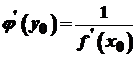 .
.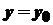 деякий приріст
деякий приріст 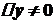 . Тоді функція
. Тоді функція 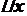 . Оскільки
. Оскільки  . Отже,
. Отже, 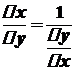 .
. , то за неперервністю функції
, то за неперервністю функції 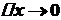 . Звідси маємо
. Звідси маємо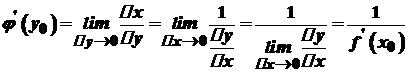 .
. . За означенням функції
. За означенням функції 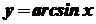
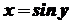 .
.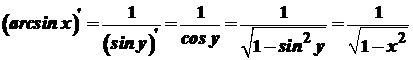 .
.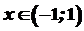 виконуються співвідношення
виконуються співвідношення 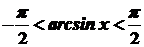 , тобто
, тобто  . Отже,
. Отже, 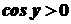 , а тому
, а тому 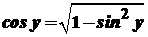 . Точки
. Точки 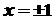 не розглядаються, так як
не розглядаються, так як 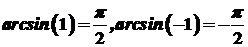 і
і 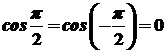 .
.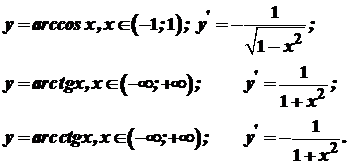
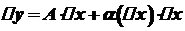 ,
,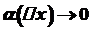 при
при 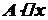 є головною частиною приросту функції, яка лінійно залежить від
є головною частиною приросту функції, яка лінійно залежить від 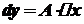 .
.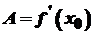 , маємо
, маємо 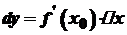 .
.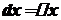 .
.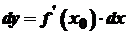 .
.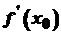 можна обчислити як відношення диференціалів:
можна обчислити як відношення диференціалів: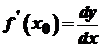 .
.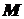 (рис. 21) на графіку функції
(рис. 21) на графіку функції  , де
, де 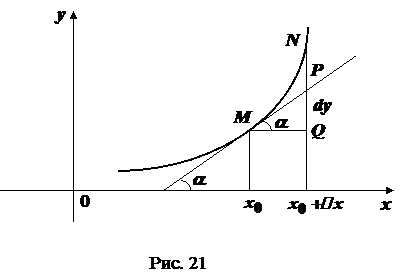


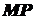 - дотична до графіка функції в точці
- дотична до графіка функції в точці 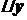 в точці
в точці 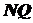 . Оскільки
. Оскільки 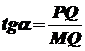 і
і 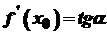 , то, враховуючи, що
, то, враховуючи, що 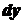 функції
функції 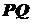 .
.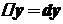 , тобто
, тобто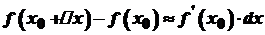 .
. (1)
(1)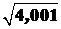 .
. . Покладемо
. Покладемо 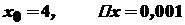 . Тоді
. Тоді  . Далі маємо
. Далі маємо  .
.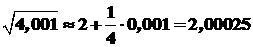 .
.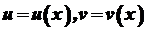 диференційовані, то мають місце наступні формули:
диференційовані, то мають місце наступні формули: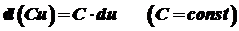 ,
,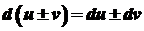 ,
,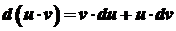 ,
,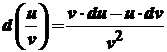 .
.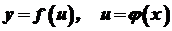 , де
, де 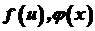 диференційовані функції в точках
диференційовані функції в точках 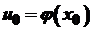 . Тоді
. Тоді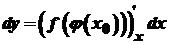 .
.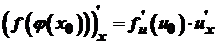 ,
,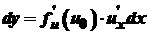 .
.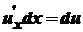 , то маємо
, то маємо 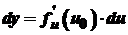 .
.