
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Поняття первісної функції та невизначеного інтеграла
Однією із основних задач диференціального числення є знаходження похідної Відтворення функції за відомою її похідною - одна із основних задач інтегрального числення. Функція
Якщо Нехай первісною функції
(
Отже, згідно з теоремою Лагранжа Таким чином, множина первісних функції Означення. Сукупність усіх первісних функції Невизначений інтеграл інакше називають інтегралом Ньютона - Лейбніца. Якщо
Знак Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.
Основні властивості невизначеного інтеграла
1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції. 
2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
3. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної постійної.
4. Сталий множник можна виносити за знак інтеграла, тобто, якщо k = const ¹ 0, то
Для доведення цієї властивості досить показати, що права чстина рівності є первісною підінтегральної функції:
5. Невизначений інтеграл від суми (різниці) функцій дорівнює сумі (різниці) невизначених інтегралів від кожної функції, тобто
Доведення.
Таблиця основних інтегралів
Безпосередньо із означення визначеного інтеграла випливають наступні формули, котрі утворюють таблицю основних інтегралів:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
Безпосереднє інтегрування
Обчислення інтегралів за допомогою безпосереднього використання таблиці основних інтегралів та їх властивостей називається безпосереднім інтегруванням. Приклади.
1.
2. 4. Метод підстановки В основі методу підстановки (методу заміни змінної) лежить формула диференціювання складеної функції. Якщо F ′( x) = f(x), хÎ(a, b), то для довільної диференційованої на проміжку (a, b ) функції x= j(t), де j(t) Î(a, b), якщо t Î(a, b ) маємо:
(F(j(t)))′ = F ′( x) j′(t) = f(x) j′(t) = f(j(t)) j′(t).
Таким чином,
тобто
Приклади. 1. Обчислити інтеграл Розв’язування. Покладемо
2. Обчислити інтеграл Розв’язування. Покладемо
Інтегрування частинами
Нехай функції
Звідси маємо
Припустимо, що інтеграл
Оскільки
Довільну сталу С включає в себе інтеграл Формула (1) називається формулою інтегрування частинами. За цією формулою обчислюються , зокрема інтеграли виду
1)
де
2)
Тут також Приклади.
ЛЕКЦІЯ 24
34. Подання раціональних дробів у вигляді суми найпростіших дробів. 35. Інтегрування найпростіших раціональних дробів.
1. Подання раціональних дробів у вигляді суми найпростіших дробів
Розглянемо дробово-раціональну функцію многочлен n-го степеня, а
де r < k. Наприклад,
У вищій алгебрі доводиться, що кожний многочлен можна подати у вигляді добутку
де А -коефіцієнт при старшому членові многочлена
де
де Ураховуючи всі комплексні корені многочлена
де Дріб Теорема. Правильний раціональний дріб
можна єдиним чином подати у вигляді суми найпростіших дробів
де Подання, про яке йдеться у наведеній теоремі, можна виконати методом невизначених коефіцієнтів, котрий розглянемо на наступному прикладі. Приклад. Розкласти на найпростіші дроби
Розв’язування. Згідно з наведеною теоремою маємо:
де Зведемо праву частину останньої рівності до спільного знаменника.
Два многочлени тотожно рівні між собою тоді й тільки тоді, коли рівні між собою коефіцієнти при однакових степенях х. Тому для визначення коефіцієнтів
Розв’язавши цю систему, одержимо:
Отже,
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 417. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

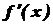 заданої функції
заданої функції 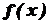 . Різноманітні питання математичного аналізу і його застосувань приводять до оберненої задачі: для даної функції
. Різноманітні питання математичного аналізу і його застосувань приводять до оберненої задачі: для даної функції 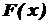 , похідна якої рівна
, похідна якої рівна 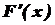 =
= 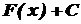 , де С - довільна стала, також є первісною для функції
, де С - довільна стала, також є первісною для функції 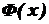 , тобто
, тобто 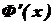 =
= 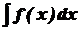 .
.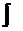 називається знаком невизначеного інтеграла,
називається знаком невизначеного інтеграла, 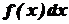 - підінтегральним виразом.
- підінтегральним виразом.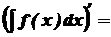 (
( 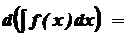 d(
d( 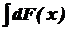 =
= 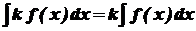 .
.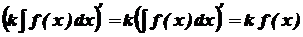 .
.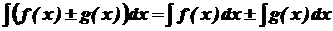 .
.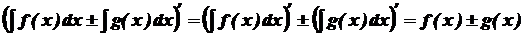 .
.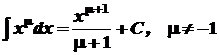 ,
,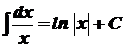 ,
,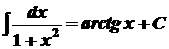 ,
,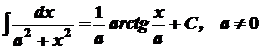
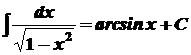 ,
,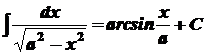 ,
,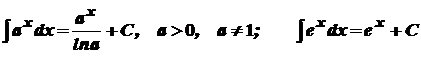 ,
,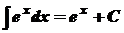 ,
,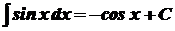 ,
,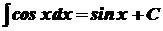 ,
,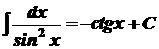 ,
,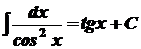 ,
,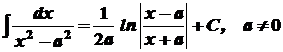 ,
,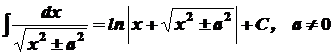
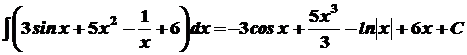 .
.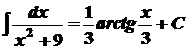 . 3.
. 3. 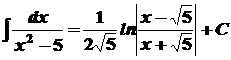 .
.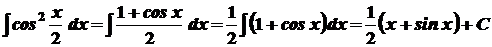 .
.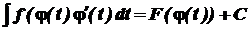 ,
,
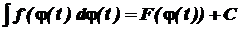 .
.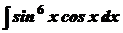 .
.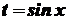 ,
, 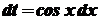 . Тоді
. Тоді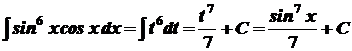 .
.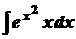 .
.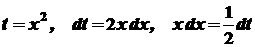 . Отже,
. Отже,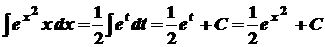 .
.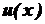 і
і 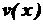 визначені й диференційовані на деякому проміжку Х. Тоді
визначені й диференційовані на деякому проміжку Х. Тоді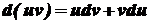 .
.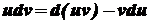 .
.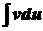 існує. Тоді
існує. Тоді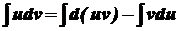 .
.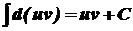 , то
, то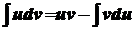 . (1)
. (1)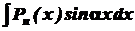 ,
, 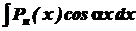 ,
, 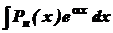 ,
,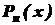 - многочлен n-ного степеня відносно х,
- многочлен n-ного степеня відносно х, 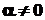 . Тут слід прийняти
. Тут слід прийняти 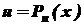 .
.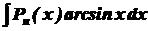 ,
, 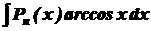 ,
,  ,
, 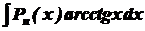 ,
, 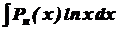
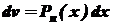 .
.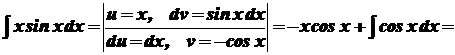
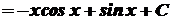 .
.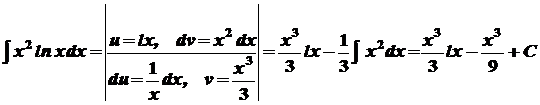 .
.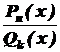 , де
, де 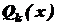 - многочлен k-го степеня. Якщо n³ k, то, виконавши ділення, одержимо
- многочлен k-го степеня. Якщо n³ k, то, виконавши ділення, одержимо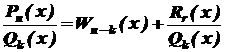 ,
,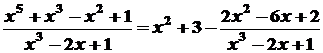 .
.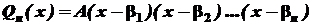 , (1)
, (1)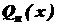 , а
, а 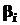 - корені рівняння
- корені рівняння 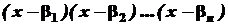 називаються елементарними. Якщо серед них є однакові, то групуючи їх, одержимо
називаються елементарними. Якщо серед них є однакові, то групуючи їх, одержимо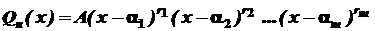 , (2)
, (2)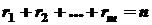 . Числа
. Числа 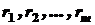 називаються кратностями коренів
називаються кратностями коренів 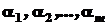 . Серед коренів
. Серед коренів 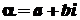
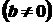 - r-кратний комплексний корінь многочлена з дійсними коефіцієнтами, то цей многочлен має також спряжений з
- r-кратний комплексний корінь многочлена з дійсними коефіцієнтами, то цей многочлен має також спряжений з 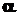 r-кратний корінь
r-кратний корінь 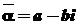 . Отже, якщо формула (2) містить множник
. Отже, якщо формула (2) містить множник 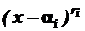 , де
, де 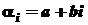
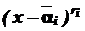 . Перемноживши ці множники, одержимо
. Перемноживши ці множники, одержимо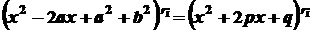 ,
,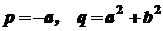 ,
, 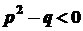 , p, q - дійсні числа.
, p, q - дійсні числа.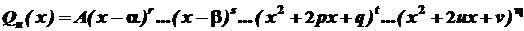 ,
,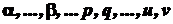 - дійсні числа.
- дійсні числа.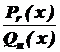 , де r < n називається правильним раціональним дробом.
, де r < n називається правильним раціональним дробом.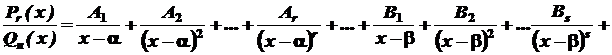
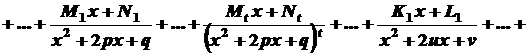
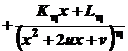 ,
,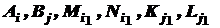 - дійсні числа.
- дійсні числа.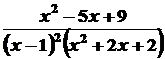 .
.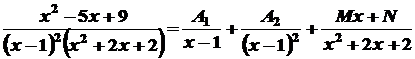 ,
,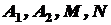 - поки що невідомі числа.
- поки що невідомі числа.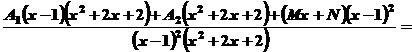
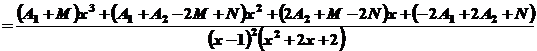
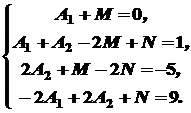
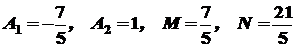 .
.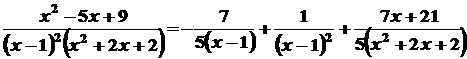 .
.