
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Наслідки з теореми Лагранжа.1. Якщо функція Враховуючи, що похідна від сталої функції дорівнює нулю, що було установлено раніше, і сформульований щойно наслідок. можна сформулювати критерій сталості диференційованої на заданому проміжку функції: Для того, щоб функція 3) Якщо функції
Теорема Коші
Теорема.Якщо функції 2) диференційовані на інтервалі то існує точка Доведення. Побудуємо допоміжну функцію
Легко перевірити, що ця функція задовольняє всім умовам теореми Ролля:
то
Звідси маємо
Одержана формула називається формулою Коші або узагальненою формулою скінчених приростів. Зауваження. У формулі Коші
ЛЕКЦІЯ 19
22. Розкриття невизначеностей. Правило Лопіталя. 2.Застосування правила Лопіталя при розкритті невизначеностей вигляду Розкриття невизначеностей. Правило Лопіталя. Теорема 1 ( правило Лопіталя). Нехай функції
 Доведення. Доозначимо в точці
де
Зауваження. Якщо похідні
Теорема 1 справджується й тоді, коли
Для доведення цього твердження достатньо покласти Теорема 2 (правило Лопіталя). Нехай функції
Доведення цієї теореми можна прочитати, наприклад, в книзі Г. М. Фихтенгольца “Основы математического анализа”, т. 1. - М.: Наука, 1964. Теорема 2 має місце також, коли Правило Лопіталя дає можливість розкривати невизначеності типу
Приклади. 1. 2.
2. Застосування правила Лопіталя при розкритті невизначеностей вигляду
Правило Лопіталя можна застосовувати при розкритті невизначеностей вигляду
Приклади. 1.
2.
3. 4. Знайдемо Отже, 5. Знайдемо
Отже,
ЛЕКЦІЯ 20
23. Формула Тейлора для многочлена. 24. Формула Тейлора для довільної функції.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 421. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 на відрізку
на відрізку  , має похідну
, має похідну 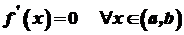 , то на відрізку
, то на відрізку  , була сталою, необхідно і достатньо, щоб її похідна
, була сталою, необхідно і достатньо, щоб її похідна 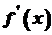 була рівною нулю в усіх точках цього проміжку.
була рівною нулю в усіх точках цього проміжку.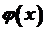 неперервні на проміжку
неперервні на проміжку 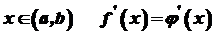 , то функція
, то функція 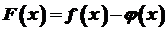 є сталою, тобто
є сталою, тобто 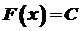 , де
, де 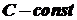 .
.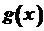 1) неперервні на відрізку
1) неперервні на відрізку  ,
,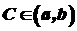 така, що
така, що 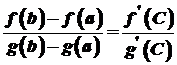 .
.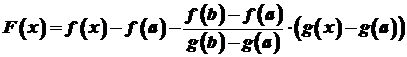 .
.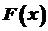 неперервна на
неперервна на 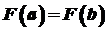 . Отже, за теоремою Ролля існує точка
. Отже, за теоремою Ролля існує точка 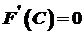 . Оскільки
. Оскільки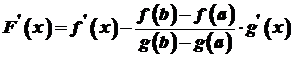 ,
,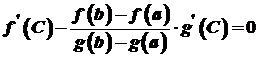 .
.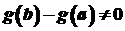 тому, що за умови
тому, що за умови  , згідно з теоремою Ролля існувала б точка
, згідно з теоремою Ролля існувала б точка 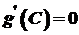 , що суперечить умові
, що суперечить умові 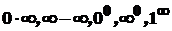 .
. і
і  . Нехай, крім того, в проміжку
. Нехай, крім того, в проміжку 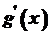 , причому
, причому 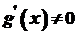 . Тоді, якщо існує границя
. Тоді, якщо існує границя 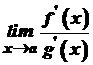 , то існує й границя
, то існує й границя 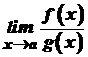 , причому
, причому .
.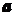 функції
функції 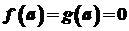 . Тоді на відрізку
. Тоді на відрізку 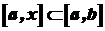 функції
функції 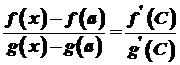 ,
,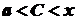 . Якщо
. Якщо 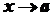 , то зрозуміло, що й
, то зрозуміло, що й  . Враховуючи, що
. Враховуючи, що 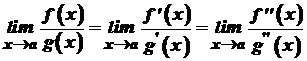 .
.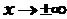 . Нехай функції
. Нехай функції 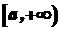 ,
, 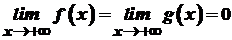 , і в проміжку
, і в проміжку 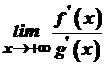 , то існує й границя
, то існує й границя 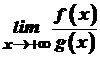 , причому
, причому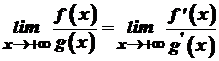 .
.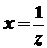 і застосувати теорему 1.
і застосувати теорему 1.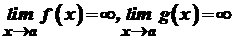 і в проміжку
і в проміжку  .
.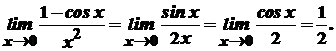
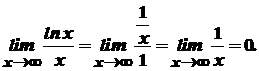

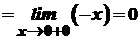 .
.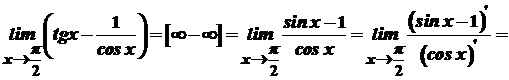
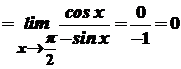 .
.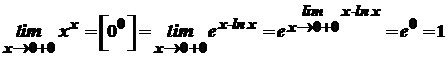 .
.

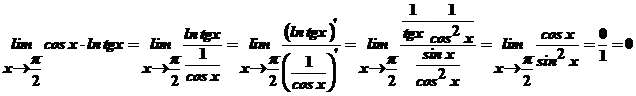 .
.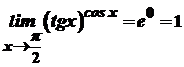 .
.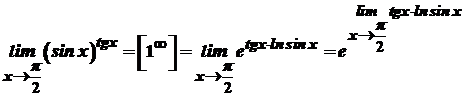 .
.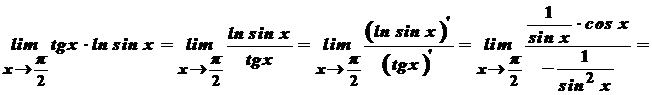
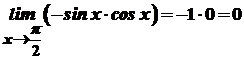 .
.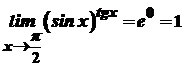 .
.