
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Інтегрування найпростіших раціональних дробів
Розглянемо інтеграли від найпростіших ірраціональних дробів.
1.
2.
3.
Тут многочлен
Уведемо підстановку
Перший із інтегралів правої частині, обчислюється безпосередньо
Другий інтеграл обчислюється за формулою 4) таблиці основних інтегралів.
36.
Увівши підстановку
Перший із інтегралів правої частини легко зводиться до інтегралу 1) таблиці основних інтегралів, а другий інтеграл
обчислюється за рекурентною формулою
ЛЕКЦІЯ 25
37. Інтегрування ірраціональних функцій. 38. Інтегрування деяких тригонометричних функцій.
Інтегрування ірраціональних функцій
Інтеграл від ірраціональної функції не завжди обчислюється в скінченному вигляді. Проте деякі типи таких інтегралів за допомогою певних підстановок можна звести до інтегралів від раціональних функцій. Позначимо
Інтеграли виду
де
де k - спільний знаменник дробів Приклад 1.Обчислити
Розв’язування. Зробимо підстановку
Далі маємо
Приклад 2.Обчислити Розв’язування.

Інтеграли виду Якщо
де знаки можна брати у будь-якій послідовності. Якщо у тричлені
У випадку коли
або
Зазначимо, що підстановки Ейлера часто приводять до досить складних раціональних функцій, а тому на практиці при обчисленні інтегралів цього типу користуються простішими методами.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
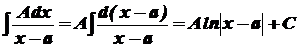 .
.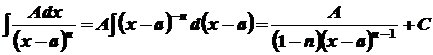 .
.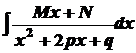 .
.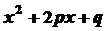 не має дійсних коренів , отже
не має дійсних коренів , отже 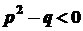 . Виділимо повний квадрат
. Виділимо повний квадрат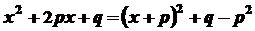 .
.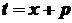 . Тоді
. Тоді 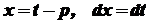 . Далі покладемо
. Далі покладемо 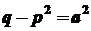 . Маємо:
. Маємо: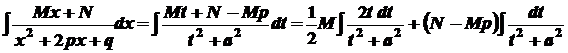 .
.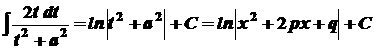 .
.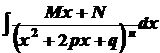 .
.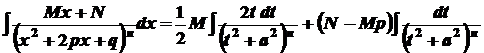 .
.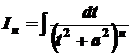
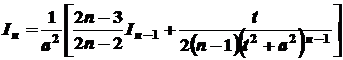 .
.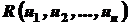 раціональну функцію від змінних
раціональну функцію від змінних 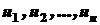 . Наприклад, функція
. Наприклад, функція 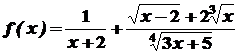 є раціональною від
є раціональною від 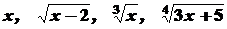 , тобто
, тобто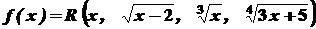 .
.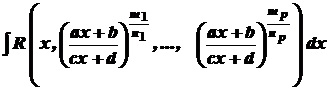 ,
,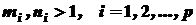 - натуральні числа,
- натуральні числа, 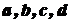 - дійсні числа, причому
- дійсні числа, причому 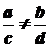 (у іншому випадку
(у іншому випадку 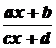 - стала величина) обчислюється за допомогою введення нової змінної
- стала величина) обчислюється за допомогою введення нової змінної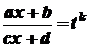 ,
,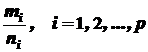 .
.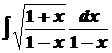 .
.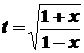 . Одержимо
. Одержимо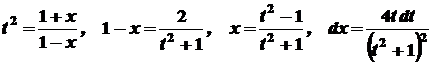 .
.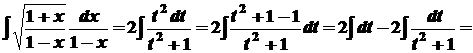

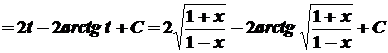 .
.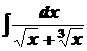 .
.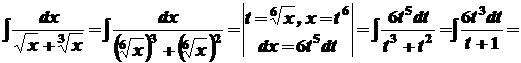
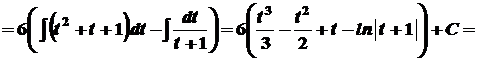
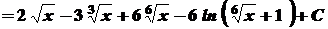 .
.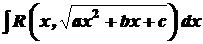 зводяться до інтегралів від раціональних функцій за допомогою підстановок Ейлера.
зводяться до інтегралів від раціональних функцій за допомогою підстановок Ейлера.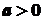 , то вводиться нова змінна t :
, то вводиться нова змінна t :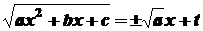 ,
,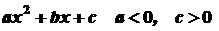 , то можна використати іншу підстановку
, то можна використати іншу підстановку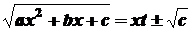 .
.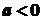 і тричлен має дійсні різні корені
і тричлен має дійсні різні корені 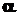 й
й 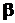 , то використовується підстановка
, то використовується підстановка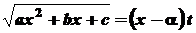
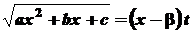 .
.