Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Похідні й диференціали вищих порядків
Похідна Приклад. Знайти похідну другого порядку функції Розв'язування.
Похідна першого порядку від похідної другого порядку називається третьою похідною, або похідною третього порядку і т. д. Якщо визначена похідна
Похідні, починаючи з похідної другого порядку, називаються похідними вищих порядків.
Формули п- них похідних деяких функцій. Нехай маємо функцію
Отже, похідну
Аналогічно можна одержати формулу для обчислення
Обчислимо
Нехай маємо показникову функцію
Зокрема,
3. Формула Лейбніца для п-ної похідної добутку двох функцій.
Нехай
Праві частини одержаних рівностей подібні на розвинення бінома
Зауваження. Доведення викладених вище формул похідних проводиться методом математичної індукції.  Диференціали вищих порядків.
Нехай функція y = f (x) диференційована в кожній точці є функцією двох змінних: аргументу
Диференціал
Диференціал Методом математичної індукції можна встановити, що
Із останньої формули випливає, що
або в іншій редакції
ТЕМА 5. ЗАСТОСУВАННЯ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ ДО ДОСЛІДЖЕННЯ ФУНКЦІЙ
ЛЕКЦІЯ 18
17. Теореми про середнє значення. 18. Теорема Ферма. 19. Теорема Ролля. 20. Теорема Лагранжа. 21. Теорема Коші.
Теореми про середнє значення
Важливе значення у курсі математичного аналізу мають так звані теореми про середнє значення диференціального числення, в яких під знаком похідної знаходиться середнє значення незалежної змінної, котре взагалі нам невідоме. Воно і похідній надає, в деякому розумінні, середнє значення. У зв’язку з цим усі ці теореми називають “теоремами про середнє”. Теорема Ферма
Теорема. Нехай функція Доведення. Нехай для визначеності функція функція За означенням похідної
причому ця границя не залежить від того, як
Якщо ж
Отже,
Звідси випливає, що Аналогічно розглядається випадок, коли в точці Обертання в нуль похідної в точці
Зауваження. Теорема Ферма справедлива, коли Теорема Ролля
Теорема.Якщо функція 1) неперервна в кожній точці відрізка 2) диференційована на інтервалі 3) на кінцях відрізка то існує точка Доведення. Оскільки функція Якщо Якщо Так як функція Із теореми Ролля випливає, що для функції
Теорема Лагранжа
Якщо функція 1) неперервна в кожній точці відрізка 2) диференційована на інтервалі
Доведення. Розглянемо допоміжну функцію
Ця функція визначена на відрізку 1) оскільки 2) функція
3) на кінцях відрізку
За теоремою Ролля існує точка
Звідси маємо
Зауваження. Якщо функція
Ця формула називається формулою скінчених приростів або формулою Лагранжа. Якщо в цій формулі покласти
Геометричний зміст теореми Лагранжа полягає в наступному. Якщо функція
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 415. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
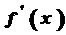 функції
функції 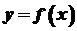 сама є деякою функцією аргументу
сама є деякою функцією аргументу 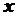 . Отже, можна ставити питання про існування похідної від функції
. Отже, можна ставити питання про існування похідної від функції  або
або 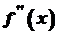 . Отже,
. Отже, 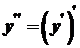 .
.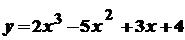 .
. ,
,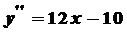 .
.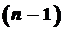 - го порядку функції
- го порядку функції  - го порядку називається перша похідна похідної
- го порядку називається перша похідна похідної  .
.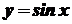 , тоді
, тоді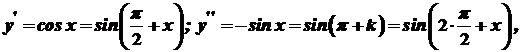
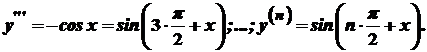
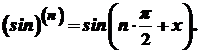
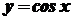
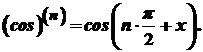
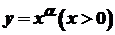 .
.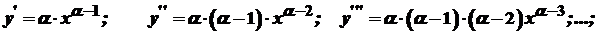
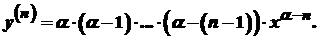
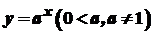 . Послідовно диференціюючи цю функцію, одержуємо
. Послідовно диференціюючи цю функцію, одержуємо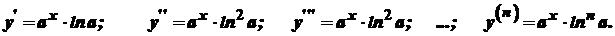

 , де
, де 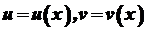 - функції, які мають похідні будь-якого порядку. Тоді
- функції, які мають похідні будь-якого порядку. Тоді

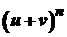 Ньютона, але замість показників степенів стоять числа, які визначають порядок похідних. При цьому самі функції
Ньютона, але замість показників степенів стоять числа, які визначають порядок похідних. При цьому самі функції  розглядаються як "похідні нульового порядку", тобто
розглядаються як "похідні нульового порядку", тобто 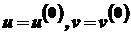 . Враховуючи це, одержуємо
. Враховуючи це, одержуємо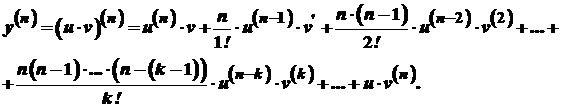
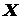 . Її диференціал першого порядку dy =f ′(x)dx
. Її диференціал першого порядку dy =f ′(x)dx  . Нехай
. Нехай 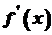 також диференційована в кожній точці
також диференційована в кожній точці 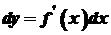 диференціал
диференціал 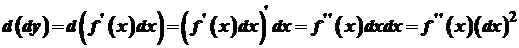 .
. називається диференціалом другого порядку і позначається
називається диференціалом другого порядку і позначається  . Отже,
. Отже,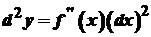 .
.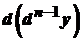 від диференціала
від диференціала  , взятий при постійному
, взятий при постійному  .
.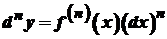 .
.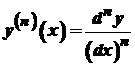 ,
, .
. визначена на інтервалі
визначена на інтервалі  і в деякій точці
і в деякій точці 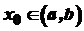 має найбільше або найменше значення. Тоді, якщо в цій точці існує похідна
має найбільше або найменше значення. Тоді, якщо в цій точці існує похідна 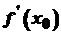 , то вона рівна нулю, тобто
, то вона рівна нулю, тобто  .
.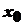 приймає найбільше значення, тобто
приймає найбільше значення, тобто 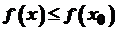 для всіх
для всіх 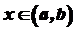 .
. ,
,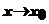 і
і 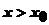 , то
, то 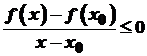 , а тому
, а тому .
.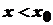 , то
, то  .
.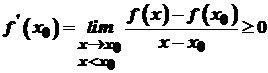 .
.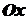 (рис. 22).
(рис. 22).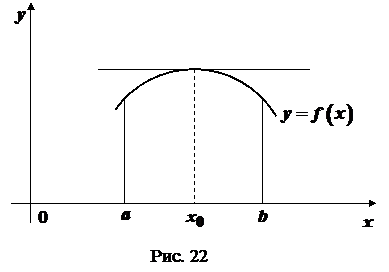
 . Наприклад, функція
. Наприклад, функція  на відрізку
на відрізку 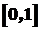 приймає найменше значення в точці
приймає найменше значення в точці  , а найбільше в точці
, а найбільше в точці 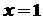 . Проте в жодній із цих точок похідна в нуль не обертається.
. Проте в жодній із цих точок похідна в нуль не обертається.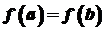 ,
,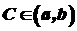 така, що
така, що 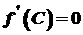 .
.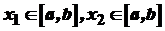 , в яких функція приймає найменше
, в яких функція приймає найменше 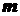 і найбільше
і найбільше 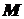 значення, тобто
значення, тобто  і
і  .
. , то функція
, то функція 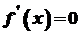 в будь-якій точці інтервалу
в будь-якій точці інтервалу 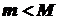 , то принаймні одне із значень
, то принаймні одне із значень 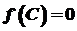 .
. паралельна вісі
паралельна вісі 
 .
.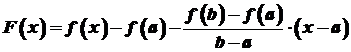 .
. неперервні функції на відрізку
неперервні функції на відрізку 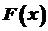 також неперервна на
також неперервна на  .
. .
.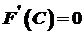 , тобто
, тобто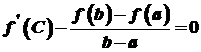 .
. .
.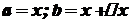 , то одержимо
, то одержимо , де
, де  .
.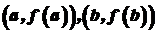 (рис. 24).
(рис. 24).