
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Необхідні й достатні умови існування екстремуми функції
Необхідна умова існування локального екстремуму функції. Якщо в точці Зазначимо, що коли функція Точки, в яких похідна функції Отже, для того, щоб функція
Достатні умови існування екстремуму функції. Теорема. Нехай 1) якщо 2) якщо 3) Якщо Доведення. 1). Нехай Доведення пунктів 2), 3) аналогічні. Із сказаного випливає правило дослідження функції на екстремум. Щоб дослідити функцію 1. Знайти область визначення функції. 2. Знайти 3. Розв’язати рівняння  4. У кожному з інтервалів 5. Розглянути знак Приклад. Дослідити наекстремум функцію
Розв’язування. 1. Функція визначена в інтервалі 2. 3. Розв’язками рівняння 4. В інтервалі 5. Точки 6. Для знаходження екстремумів функції Теорема . Нехай Доведення. Згідно з умовою теореми Випадок, коли Скориставшись формулою Тейлора, можна довести наступну теорему. Теорема. Якщо в стаціонарній точці
4. Знаходження найбільшого й найменшого значення функції на відрізку Для знаходження найбільшого й найменшого значення функції
ЛЕКЦІЯ 22
1. Опуклість та вгнутість кривої. Точки перегину. 2. Асимптоти графіка функції. 3. Загальна схема дослідження функцій і побудови їх графіків.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 468. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
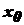 функція
функція  має екстремум, то існує окіл
має екстремум, то існує окіл  точки
точки  є найбільшим або найменшим. Отже, якщо в точці
є найбільшим або найменшим. Отже, якщо в точці 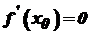 .
.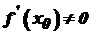 , то або
, то або 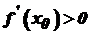 , тобто функція зростає, або
, тобто функція зростає, або 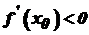 і функція спадає. Звідси випливає, що функція
і функція спадає. Звідси випливає, що функція 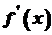 рівна нулю, або не існує.
рівна нулю, або не існує.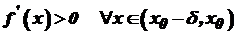 і
і 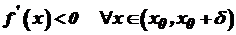 , то точка
, то точка  і
і 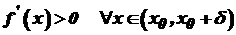 , то точка
, то точка 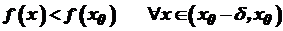 і
і  . Отже, для будь-якого
. Отже, для будь-якого 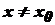 із околу
із околу 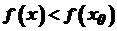 , тобто точка
, тобто точка 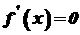 та визначити ті значення
та визначити ті значення 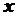 , при яких
, при яких  або
або 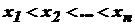 , які знаходяться в інтервалі
, які знаходяться в інтервалі  області визначення функції
області визначення функції 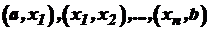 взяти довільну точку і визначити в ній знак першої похідної. Який знак матиме похідна у вибраній точці, такий же знак вона матиме й у відповідному інтервалі.
взяти довільну точку і визначити в ній знак першої похідної. Який знак матиме похідна у вибраній точці, такий же знак вона матиме й у відповідному інтервалі. .
.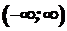 .
.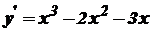 .
.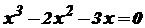 є
є 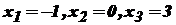 .
.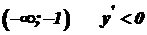 , функція спадає; в інтервалі
, функція спадає; в інтервалі  , функція зростає; інтервалі
, функція зростає; інтервалі 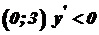 , функція спадає; в інтервалі
, функція спадає; в інтервалі 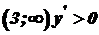 , функція зростає.
, функція зростає.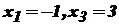 є точками мінімуму, а точка
є точками мінімуму, а точка 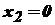 є точкою максимуму даної функції.
є точкою максимуму даної функції.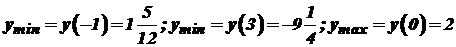 .
.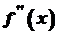 . Це випливає із наступної теореми.
. Це випливає із наступної теореми.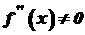 . Тоді, якщо
. Тоді, якщо 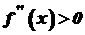 , то точка
, то точка  , то – максимуму.
, то – максимуму.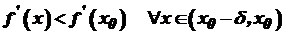 і
і 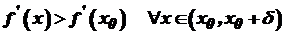 . Оскільки
. Оскільки  досліджується аналогічно.
досліджується аналогічно.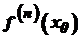 є похідною парного порядку, то точка
є похідною парного порядку, то точка 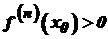 і точкою максимуму, якщо
і точкою максимуму, якщо 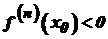 . Якщо ж перша відмінна від нуля похідна
. Якщо ж перша відмінна від нуля похідна  , потрібно знайти всі її локальні екстремуми на цьому відрізку та її значення на кінцях відрізка, тобто
, потрібно знайти всі її локальні екстремуми на цьому відрізку та її значення на кінцях відрізка, тобто 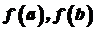 . Потім з одержаних значень вибрати найменше й найбільше.
. Потім з одержаних значень вибрати найменше й найбільше.