
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема про неперервність оберненої функції.
Нехай функція Доведення. Нехай для визначеності функція Однозначність оберненої функції Покажемо, що обернена функція Установимо тепер, що функція Лема. Якщо множина значень монотонно зростаючої (спадної) функції Щоб це довести, візьмемо точку Це і означає, що Аналогічно можна встановити неперервність функції  Перейдемо до доведення неперервності функції
ТЕМА 5. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
ЛЕКЦІЯ 15
5. Задачі, що проводять до поняття похідної. 6. Означення похідної. 7. Механічний та геометричний зміст похідної. 8. Односторонні похідні. 9. Нескінченні похідні. Задачі, що проводять до поняття похідної
Задача про миттєву швидкість. Нехай матеріальна точка Відношення Швидкістю руху точки в момент часу
Приклад. Знайти миттєву швидкість рівномірно прискореного руху матеріальної точки з початковою швидкістю Розв'язування. Залежність шляху
Після спрощення одержуємо
Таким чином
Задача про лінійну густину неоднорідного стержня. Нехай треба знайти густину неоднорідного прямолінійного стержня в точці
Відношення Лінійною густиною стержня в точці
Приклад. Нехай маса стержня довжини Розв'язування. Знайдемо приріст маси в точці
Отже,
Задача про дотичну до кривої. Дотичною до кривої
Зазначимо, що не в кожній точці крива може мати дотичну. В точках, яких крива зазнає зламу, дотична до кривої не існує. Так, наприклад, не існують дотичні у точці 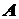 кривої кривої  (рис. 13), точці (рис. 13), точці  кривої кривої  (рис. 14), точці (рис. 14), точці 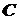 кривої кривої  (рис. 15). (рис. 15).
Розглянемо криву, яка задана в системі координат рівнянням 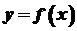 , де , де  неперервна функція, визначена на деякому проміжку неперервна функція, визначена на деякому проміжку 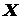 . Поставимо задачу: знайти кутовий коефіцієнт . Поставимо задачу: знайти кутовий коефіцієнт 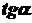 дотичної до кривої дотичної до кривої 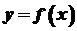 в точці в точці 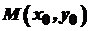 , де , де 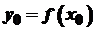 (рис. 16). (рис. 16).
Візьмемо на кривій Якщо точка
Звідси випливає, що коли точка
Розглянуті задачі різні за своїм змістом, але вони відрізняються одним і тим способом, якщо в кожній з цих задач незалежну змінну позначити через
Означення похідної Нехай в деякому проміжку Зазначимо, що Похідною функції Похідну функції
Якщо функція
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 548. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
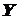 − множина значень. Тоді на множині
− множина значень. Тоді на множині 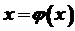 однозначна, строго монотонна та неперервна.
однозначна, строго монотонна та неперервна. , що задовольняють умову
, що задовольняють умову 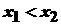 , виконується нерівність
, виконується нерівність 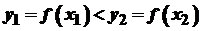 .
.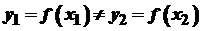 при
при 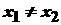 . Отже, кожному
. Отже, кожному  відповідає єдине значення
відповідає єдине значення 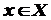 .
.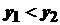 , то
, то 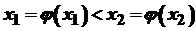 , оскільки за умови
, оскільки за умови 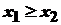 виконувалася б умова
виконувалася б умова 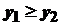 , що суперечить допущенню
, що суперечить допущенню  , котра не є його правим кінцем, і покажемо, що в цій точці функція
, котра не є його правим кінцем, і покажемо, що в цій точці функція  і їм відповідають у
і їм відповідають у  . Нехай
. Нехай 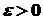 довільне, але настільки мале число, щоб значення
довільне, але настільки мале число, щоб значення 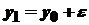 також належало проміжку
також належало проміжку 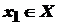 , що
, що  , причому
, причому 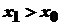 ( оскільки при
( оскільки при 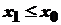 і
і  ). Покладемо
). Покладемо 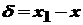 , тобто
, тобто 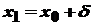 . Якщо тепер
. Якщо тепер 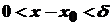 , тобто
, тобто 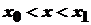 , то
, то 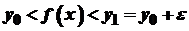 або
або 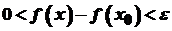 .
.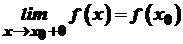 . Тобто функція
. Тобто функція 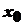 справа.
справа.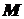 рухається вздовж прямої. Позначимо відстань точки
рухається вздовж прямої. Позначимо відстань точки  даної прямої в момент часу
даної прямої в момент часу 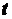 через
через 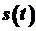 . Тоді в момент часу
. Тоді в момент часу 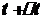 , де
, де 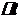 - приріст часу, точка
- приріст часу, точка 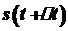 . Різницю
. Різницю 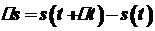 назвемо приростом шляху.
назвемо приростом шляху.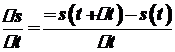 називається середньою швидкістю руху точки за проміжок часу
називається середньою швидкістю руху точки за проміжок часу 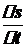 при
при 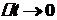 , тобто
, тобто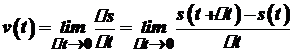 .
. і прискоренням
і прискоренням 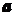 .
.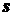 від часу
від часу 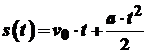 . Тоді
. Тоді 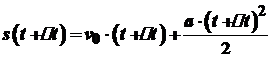 . Отже,
. Отже,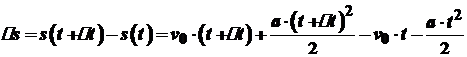 .
.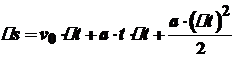 .
.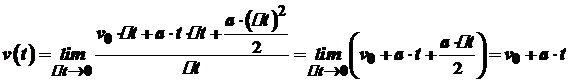 .
.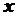 від початкової точки
від початкової точки 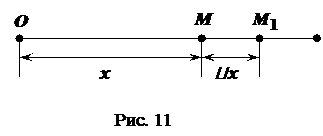 Позначимо
Позначимо 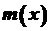 величину маси відрізка
величину маси відрізка 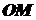 . Візьмемо деяку точку
. Візьмемо деяку точку 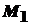 , яка знаходиться на відстані
, яка знаходиться на відстані 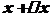 від початкової точки
від початкової точки 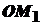 буде рівною
буде рівною  . Отже, маса відрізка
. Отже, маса відрізка  , яку ми назвемо приростом маси в точці
, яку ми назвемо приростом маси в точці  .
.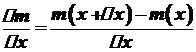 називається середньою густиною стержня на відрізку
називається середньою густиною стержня на відрізку 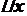 і позначається
і позначається 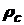 .
.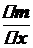 при
при 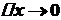 , тобто
, тобто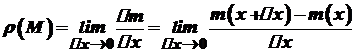 .
.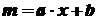 , де
, де  - сталі числа. Знайти лінійну густину в точці
- сталі числа. Знайти лінійну густину в точці 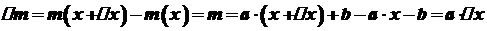 .
.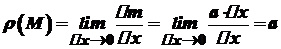 .
.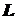 в точці
в точці 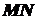 за умови, що точка
за умови, що точка 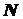 по кривій
по кривій 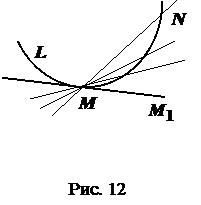

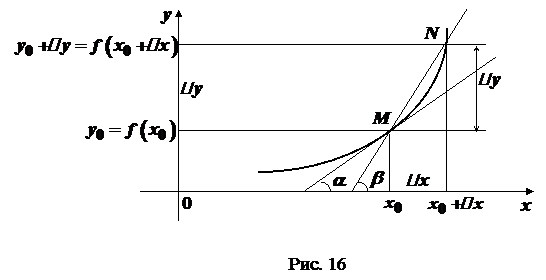
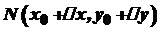 . Через точки
. Через точки 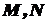 проведемо січну. Нехай вона утворює з додатним напрямом осі
проведемо січну. Нехай вона утворює з додатним напрямом осі 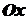 кут
кут 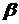 . Тоді
. Тоді 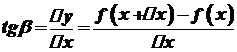 .
.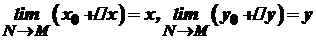 .
.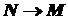 , то
, то 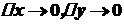 . З іншого боку, якщо
. З іншого боку, якщо  , тобто
, тобто  . Таким чином
. Таким чином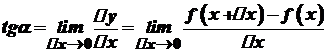 .
.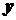 , то для знаходження розв'язку кожної із них потрібно знаходити границю відношення приросту функції до приросту аргументу, за умови, що приріст аргументу прямує до нуля, тобто
, то для знаходження розв'язку кожної із них потрібно знаходити границю відношення приросту функції до приросту аргументу, за умови, що приріст аргументу прямує до нуля, тобто .
.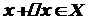 .
.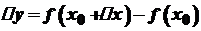 . Нехай в точці
. Нехай в точці 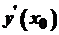 або
або 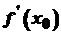 . Отже, за означенням
. Отже, за означенням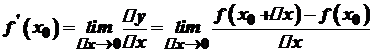 .
.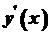 або
або 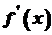 .
.