
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о существовании единственного решения задачи Коши для квазилинейных УрЧП первого порядка в случае пространственных переменных.
где
причем Задача Коши состоит в нахождении поверхности Теорема: 1) Пусть 2) 3) 4) Тогда существует окрестность кривой
(окрестности в плоскости Доказательство: ◄ Идея доказательства состоит в том, что через каждую точку
1) Продолжим Считаем, что
2) Через каждую точку
3) По теореме о непрерывности и непрерывной дифференцируемости по начальным данным получим, что принадлежит
где
то теореме об обратной функции (можно считать, что
4) Поскольку 
Положим
Очевидно, что 5. Докажем, что
Допустим, что это не так. Тогда
6) Построим решение УрЧП (1) следующим образом: пусть По второй лемме о характеристиках 7) Единственность. Путь
(Если
Оператор Штурма-Лиувилля. Его собственные функции. Лемма о нулевом собственном значении.
Область определения оператора Штурма-Лиувилля:
def: Функция 1) 2) 3)
Лемма о нулевом собственном значении оператора Штурма-Лиувилля. Лемма: Число Доказательство: ◄ (
(Если Аналогично (
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 389. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1),
(1), − функции класса
− функции класса 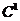 от
от  в окрестности кривой
в окрестности кривой ,
,  ,
, в этой окрестности.
в этой окрестности. класса
класса 



 , где
, где 
 вида
вида ) и единственная функция
) и единственная функция  на интервал
на интервал  при достаточно малом
при достаточно малом  так, чтобы продолжение функции
так, чтобы продолжение функции  (например линейным образом)
(например линейным образом) лежит в области определения
лежит в области определения  и
и  при
при 
 ,
,  , причем
, причем  ,
,  . Положим:
. Положим:


 определено и
определено и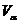
 . Поскольку
. Поскольку
 по условию 4),
по условию 4), ,
,  ,
,  (можно считать, что
(можно считать, что  настолько мало, что это выполняется
настолько мало, что это выполняется 
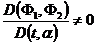 при
при 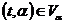 (
(  достаточно малым).
достаточно малым). − открытая окрестность точки
− открытая окрестность точки  на плоскости
на плоскости  − диффеоморфизм класса
− диффеоморфизм класса  также
также 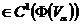 .
. − компакт в
− компакт в  и
и  , а
, а  , то
, то 




 .
. ,
,  ,
, 
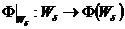 инъективно.
инъективно.

 ,
,  ,
,  . По теореме Больцано-Вейерштрассе
. По теореме Больцано-Вейерштрассе 


 и
и 
 , Так как
, Так как  . По условию 3 теоремы
. По условию 3 теоремы  (обозначение). Поскольку
(обозначение). Поскольку  при некотором
при некотором  ,
,  открыто в
открыто в  взаимно-однозначно, то
взаимно-однозначно, то  при достаточно больших
при достаточно больших  , а это противоречит выбору
, а это противоречит выбору  и
и  Противоречие! Итак
Противоречие! Итак  :
:  − диффеоморфизм класса
− диффеоморфизм класса  − открытая окрестность
− открытая окрестность  . Положим
. Положим  и
и 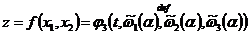 (см. 2)). Тогда
(см. 2)). Тогда 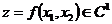 , так как
, так как  по
по  и
и  , а
, а  .
. − решение УрЧП (1), причем
− решение УрЧП (1), причем  . Проведем через
. Проведем через 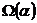 характеристику
характеристику  . По первой лемме о характеристиках
. По первой лемме о характеристиках
 ,
,  и
и  , то
, то  может
может  так как
так как  , а это продолжение не единственно) ►
, а это продолжение не единственно) ► ,
,  , (1)
, (1) (2)
(2)




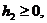




 это оператор Штурма-Лиувилля.
это оператор Штурма-Лиувилля. называется собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению
называется собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению  , если
, если

 .
. является собственным значением оператора Штурма-Лиувилля
является собственным значением оператора Штурма-Лиувилля 


 . При этом
. При этом  является собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению
является собственной функцией оператора Штурма-Лиувилля, отвечающей собственному значению  ) Пусть
) Пусть  − соответствующая собственная функция. Тогда
− соответствующая собственная функция. Тогда
 Так как
Так как 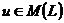 , то
, то
 .
. , например
, например  , то
, то 
 , так как
, так как 







 ) Пусть
) Пусть  ,
, 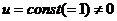 , тогда
, тогда  ,
,  , так как
, так как  и
и  ►
►