Существование полной системы первых интегралов

Теорема:

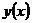       Пусть  – некоторое решение системы  (1) на 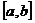. Тогда в окрестности графика  существует полная система первых интегралов системы (1).

Доказательство:

◄ Пусть  – точка на графике, а  – другая точка на графике. Тогда решение 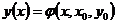. Далее 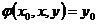. В силу единственности интегральной линии, проходящей через точку . Положим  (фиксируем 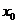), ( ). Покажем, что соотношение  – полная система первых интегралов системы (1).

Проверим 3 условия.

1) функции  определены в окрестности графика  и  по теореме о дифференцируемости по начальным данным и параметру.

2) условие 2) докажем позже.

3) Пусть  – решение системы (1), тогда , то есть условие 3) проверено.

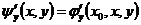Заметим, что  (матрица Якоби) – резольвента линейной системы  (здесь переменная , а  – начальные данные).

По следствию 2 теоремы о дифференцируемости решения задачи Коши по начальным данным и параметру , так как резольвента является ФМР, то есть .

Если бы , для некоторого , в некоторой окрестности из G, то  в этой окрестности, а тогда i-я строка матрицы  равнялась бы нулю 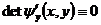 в этой окрестности, а это не так  ни в какой окрестности из G, для каждого , то есть условие 2) проверено.  – система первых интегралов, заодно доказано, что она является полной. ►