
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференцируемости решения системы ОДУ по начальным данным и параметру.Теорема:
определенное на Теперь
определенное так же на
Замечание: Формулы (5) и (6) получаются формальным дифференцированием по
Доказательство: ◄ По теореме о непрерывном решении по начальным данным и параметру существует единственное решение
где Положим
тогда
функция Далее
Теорема доказана. ► Замечание: Все сказанное справедливо при
Это уравнение называется уравнением в вариациях. Следствие 1: Пусть в предыдущей теореме
Следствие 2: Пусть в предыдущей теореме
то есть Следствие 3: Пусть в предыдущей теореме
Первые интегралы систем дифференциальных уравнений. Задание общего решения системы с помощью полной системы первых интегралов. 
Рассмотрим систему
Будем предполагать, что def: Соотношение 1) 2) 3) Если def: Система первых интегралов системы (1) Теорема: Полная система первых интегралов системы (1) задает решение системы (1) (локально). Доказательство: ◄ Пусть
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 524. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 – область в
– область в  .
.  – отрезок, а отображение
– отрезок, а отображение  непрерывно,
непрерывно,  ,
,  и
и  так же непрерывны на
так же непрерывны на 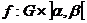 ,
,  . Далее пусть
. Далее пусть 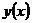 – решение задачи Коши:
– решение задачи Коши: ,
,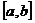 . Функции
. Функции  ,
,  ,
, 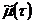

 , при некотором
, при некотором  . Причем
. Причем 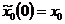 ,
,  ,
,  .
.
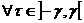 Существует единственное решение задачи Коши:
Существует единственное решение задачи Коши: ,
,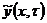 , дифференцируема по
, дифференцируема по  при
при 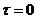 и
и 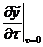 , удовлетворяет условию
, удовлетворяет условию
 (5).
(5). (6)
(6) тождества
тождества
 (то есть при
(то есть при  ). Далее
). Далее

 ,
, непрерывна при
непрерывна при  .
. ,
, является решением задачи Коши
является решением задачи Коши ,
,

 ,
, 
 . По теореме о непрерывности по начальным данным и параметру
. По теореме о непрерывности по начальным данным и параметру 
 , где
, где  – решение задачи
– решение задачи

 и
и  удовлетворяет уравнению
удовлетворяет уравнению .
.
 и
и 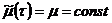 , тогда
, тогда  удовлетворяет условиям
удовлетворяет условиям
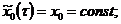

 и
и  удовлетворяет условиям
удовлетворяет условиям
 − матрица Якоби и удовлетворяет условиям
− матрица Якоби и удовлетворяет условиям

 – резольвента линейной системы
– резольвента линейной системы  .
.
 и
и  , тогда
, тогда  удовлетворяет условиям
удовлетворяет условиям
 (1).
(1). и
и 
 непрерывны в области
непрерывны в области  (
(  может не существовать).
может не существовать).
 называется первым интегралом системы (1) в области G, если выполняется 3 условия:
называется первым интегралом системы (1) в области G, если выполняется 3 условия:

 ни в какой окрестности произвольной точки из G.
ни в какой окрестности произвольной точки из G.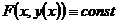 (те есть
(те есть  на графике решения системы(1))
на графике решения системы(1))
 (Якобиан) в каждой точке из G.
(Якобиан) в каждой точке из G. – произвольная точка из G, тогда соотношения
– произвольная точка из G, тогда соотношения 
 в окрестности точки
в окрестности точки 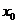 , удовлетворяющую условию
, удовлетворяющую условию  . По теореме о неявной функции (эту теорему можно применить, так как
. По теореме о неявной функции (эту теорему можно применить, так как  и
и  в окрестности точки
в окрестности точки  решения задачи Коши, существует единственное решение
решения задачи Коши, существует единственное решение  системы (1), удовлетворяющее начальному условию
системы (1), удовлетворяющее начальному условию  (
(  , так как по предположению
, так как по предположению 
 в окрестности точки
в окрестности точки