
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема Ляпунова об асимптотической устойчивости по линейному приближению.
Рассмотрим систему Далее, пусть Доказательство: ◄ Мы сведем эту теорему к проверке выполнимости условия леммы Ляпунова об асимптотической устойчивости. По лемме: существует матрица T
где
(a – из условия теоремы). Положим
Положим: 1) 2) Осталось проверить условие: 3) Заметим, что 1) 2) Проверку условия 3) проведем в 3 этапа. Сделаем некоторые оценки. Пусть
тогда
Аналогично
Запишем подробно систему (2):
Пусть
Оценим каждое
при достаточно малых Возьмем произвольную точку
То есть выполняется условие леммы Ляпунова об асимптотической устойчивости. Следовательно нулевое решение системы (1) асимптотически устойчиво. ►
Лемма Адамара. Лемма: Пусть 
Тогда Доказательство: ◄ По формуле Ньютона-Лейбница
Непрерывность
Замечание 1: Замечание 2: Если
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 505. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1). Пусть A – постоянная матрица с действительными коэффициентами, размера
(1). Пусть A – постоянная матрица с действительными коэффициентами, размера  . А
. А  – n-мерная действительная вектор-функция, непрерывная по y в полуцилиндре:
– n-мерная действительная вектор-функция, непрерывная по y в полуцилиндре:  , причем
, причем  – не зависит от x, где
– не зависит от x, где  при
при 
 .
. , где
, где  – собственное значение матрицы A
– собственное значение матрицы A  (некоторые могут совпадать),
(некоторые могут совпадать),  . Тогда нулевое решение системы (1) асимптотически устойчиво.
. Тогда нулевое решение системы (1) асимптотически устойчиво. : матрица
: матрица  будет иметь вид:
будет иметь вид: ,
,
 , подставим в (1):
, подставим в (1):


 (2).
(2). ,
,  . Выполняется условие леммы Ляпунова об асимптотической устойчивости:
. Выполняется условие леммы Ляпунова об асимптотической устойчивости: – верно,
– верно, ,
,  ,
, .
. ,
, ,
,  .
. ,
,  ,
,


 .
. (3)
(3)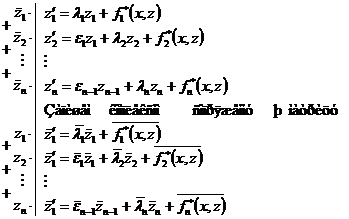
 – решение системы (1), а
– решение системы (1), а  – решение системы (2), тогда
– решение системы (2), тогда


 .
. .
.
 .
.

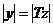 , так как
, так как  (то есть
(то есть 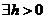
 ,
, 
 ).
).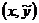 из полуцилиндра
из полуцилиндра  , поскольку через эту точку проходят интегральная линия
, поскольку через эту точку проходят интегральная линия 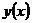 (по теореме о
(по теореме о  решения задачи Коши), то в этой точке будет
решения задачи Коши), то в этой точке будет

 +
+  =
=  ,
, .
. – выпуклая область в
– выпуклая область в  (то есть
(то есть  отрезок, соединяющий
отрезок, соединяющий  и
и  ).
).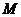 – метрическое пространство, а функции
– метрическое пространство, а функции 
 и
и  ,
,  непрерывны на
непрерывны на  .
. ,
, 
 , где
, где  непрерывна на
непрерывна на  ,
,  .
. =
=  =
= =
=  .
. вытекает из непрерывность интеграла по параметру (по теореме из математического анализа). ►
вытекает из непрерывность интеграла по параметру (по теореме из математического анализа). ► (надо подставить
(надо подставить  имеет непрерывные смешанные производные по
имеет непрерывные смешанные производные по  до порядка
до порядка  включительно и эти производные непрерывны на
включительно и эти производные непрерывны на  имеет непрерывную смешанную производную по
имеет непрерывную смешанную производную по  (
(  ) до порядка
) до порядка  включительно и эти производные непрерывны на
включительно и эти производные непрерывны на