
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Устойчивость решения по Ляпунову и асимптотическая устойчивость. Лемма Ляпунова об устойчивости.
Рассмотрим систему:
Будем предполагать, что 1) 2)
def: Решение def: Решение 1) Оно устойчиво по Ляпунову; 2)
Пример 1:
Пример 2:
Это затухающие колебания, нулевое решение асимптотически устойчиво.
Замечание: Исследовать устойчивость (асимптотическую) решения Положим: тогда
Лемма Ляпунова об устойчивости. Пусть функция 1) 2) 3) Тогда нулевое решение системы
Доказательство:
◄ Фиксируем Замечание: Функция 
Лемма Ляпунова об асимптотической устойчивости и ее усиленный вариант.
Пусть выполнены условия леммы Ляпунова об устойчивости. Далее пусть
1) 2) 3) Тогда нулевое решение асимптотически устойчиво. Доказательство: ◄ Сначала докажем усиленный вариант леммы Ляпунова об асимптотической устойчивости. Усиленный вариант. Пусть выполняется условие леммы Ляпунова об устойчивости. Далее пусть существует семейство непрерывных функций 1) 2) Тогда нулевое решение системы (1) асимптотически устойчиво. Доказательство: ◄ Фиксируем Пусть Как было показано в доказательстве предыдущей леммы функция Так как
Перейдем к доказательству леммы Ляпунова об асимптотической устойчивости (в качестве следствия). Достаточно положить 1) 2) Если
Лемма по приведению матрицы к жордановой форме с ε вместо 1 под диагональю. Пусть B – матрица, имеющая жорданову форму, то есть:
Тогда
Докажем это для одной клетки. Доказательство: ◄ Известно, что замена переменной
Положим
Подставим это в систему
Лемма доказана. ►
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 686. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1).
(1). решение
решение  системы (1) на участке
системы (1) на участке  , при условии
, при условии  ;
;
 ,
,  ,
,  на участке
на участке  .
.
 ,
,  ,
, 
 . Другими словами, устойчивость по Ляпунову – это непрерывная зависимость решения от изначально данного
. Другими словами, устойчивость по Ляпунову – это непрерывная зависимость решения от изначально данного  , равномерная на луче
, равномерная на луче  при
при  .
. – маятник без трения. Нулевое решение устойчиво, но не асимптотически устойчиво:
– маятник без трения. Нулевое решение устойчиво, но не асимптотически устойчиво:  .
. – маятник с трением.
– маятник с трением.

 ,
,
 . В дальнейшем будем исследовать устойчивость (асимптотическую) только нулевого решения.
. В дальнейшем будем исследовать устойчивость (асимптотическую) только нулевого решения. – непрерывна по x и локально удовлетворяет условию Липшица по y,
– непрерывна по x и локально удовлетворяет условию Липшица по y, 
 . Далее пусть
. Далее пусть  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
 ;
; ;
;
 тогда
тогда 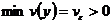
 в силу 2). Поскольку
в силу 2). Поскольку  непрерывна в точке 0 и
непрерывна в точке 0 и  , то
, то 


 .Покажем, что это
.Покажем, что это  искомое, то есть
искомое, то есть 

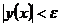 , где
, где 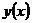 – решение системы (1) с начальным условием
– решение системы (1) с начальным условием 
 . Положим
. Положим  , тогда
, тогда 
 в силу 3). То есть
в силу 3). То есть  не возрастает (по теореме Лагранжа). С другой стороны
не возрастает (по теореме Лагранжа). С другой стороны 
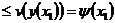

 – противоречие ►
– противоречие ►
 удовлетворяет следующим условиям:
удовлетворяет следующим условиям: ;
; ;
; .
.
 удовлетворяет следующим условиям:
удовлетворяет следующим условиям: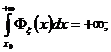
 ,
,  .
. ,
, 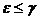 , тогда
, тогда 

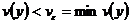
 и
и  . Покажем, что
. Покажем, что  , при
, при 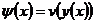 не возрастает, заметим, что
не возрастает, заметим, что  , так как
, так как  . По теореме из анализа
. По теореме из анализа  . Покажем, что
. Покажем, что  . Допустим
. Допустим  тогда в силу непрерывности функции
тогда в силу непрерывности функции 

 . В этом случае
. В этом случае 
 (если бы
(если бы  для некоторого
для некоторого  ,то
,то  , а у нас
, а у нас  , то есть
, то есть  ).
).  (условие 2) для семейства
(условие 2) для семейства  ).
).

 (условие 1))
(условие 1))  , при
, при  , а у нас
, а у нас  , при
, при  ,
, 
 в этом случае
в этом случае 

 . А у нас доказано, что
. А у нас доказано, что  при
при  . Очевидно, что:
. Очевидно, что: то
то  .
. 


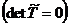 такая, что
такая, что
 переводит систему
переводит систему  в систему
в систему  . Построим
. Построим 
 .
.