
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные системы с постоянными коэффициентами и методы их решения Случай не нормализуемой системы.
II случай: Заметим, что Распишем:
столбцы линейно зависимы. Можно считать после перенумерования, что линейно зависимы первые k столбцов
…
…
При такой замене гладкость не изменилась. Обратная замена:
В матричной форме:
подставим в систему (1):
Здесь Определитель не изменился. Покажем, что порядок системы понизился, то есть
итак, в новой системе
Если полученная система оказалась нормализуемая, то для этой новой системы гладкость решения обоснована, а тогда она обоснована для решения “старой” системы. Если же новая система также не нормализуема, то повторяем для нее предыдущие рассуждения. Получим систему, в которой Замечание 1: В общем решении системы (1) произвольных постоянных столько, какова степень Пример:
Замечание 2: Если Пример:
Нормальные линейные системы с постоянными коэффициентами и методы их решения
(рассмотрим только однородные системы) 
Из алгебры известно, что
Сделаем замену неизвестных функций
Положим
где Итак, если матрица T известна, то общее решение системы (1) равно сумме (для всех клеток) выражений типа (3). Обычно матрицу T трудно найти. Для получения общего решения системы (1) используем формулу (3), где Подставим y из (3) в (1):
Эта система похожа на систему (2), то есть неизвестных
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 468. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (случай не нормализуемой системы).
(случай не нормализуемой системы).  +младшие степени p.
+младшие степени p.


 , причем
, причем  ,
,  ;
;  . Сделаем замену неизвестных функций:
. Сделаем замену неизвестных функций: – можно дифференцировать
– можно дифференцировать 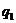 раз
раз – можно дифференцировать
– можно дифференцировать  раза
раза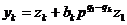 – можно дифференцировать
– можно дифференцировать  раза
раза – можно дифференцировать
– можно дифференцировать  раз
раз – можно дифференцировать
– можно дифференцировать  раз.
раз.
 , где
, где
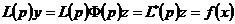

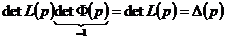 .
. . Запишем i-е уравнение новой системы:
. Запишем i-е уравнение новой системы:

 ,
, , то есть порядок системы понижен.
, то есть порядок системы понижен. , а
, а 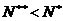 . За конечное число шагов получим нормализуемую систему (если
. За конечное число шагов получим нормализуемую систему (если  ).
). при
при  нет констант.
нет констант. , то система может иметь бесконечно много решений, а так же может не иметь ни одного решения.
, то система может иметь бесконечно много решений, а так же может не иметь ни одного решения. если
если  , то
, то  может быть любой функцией класса
может быть любой функцией класса 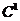 , а
, а  . Если
. Если  , то система не имеет ни одного решения.
, то система не имеет ни одного решения. (1)
(1) ,
,  .
. – матрица
– матрица  ,
,  , так же, что
, так же, что  имеет жорданову форму:
имеет жорданову форму:
 и подставим в систему (1)
и подставим в систему (1)  ,
, 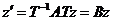 . Система распалась на несколько независимых систем (их стало столько, сколько жордановых клеток в матрице B). Будем исследовать одну клетку, например
. Система распалась на несколько независимых систем (их стало столько, сколько жордановых клеток в матрице B). Будем исследовать одну клетку, например  , причем пусть ее порядок
, причем пусть ее порядок  равен максимальному порядку всех клеток, отвечающих
равен максимальному порядку всех клеток, отвечающих  (2).
(2). и подставим в (2):
и подставим в (2):


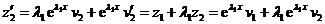




 (3),
(3), .
. – неизвестные n-мерные векторы.
– неизвестные n-мерные векторы.

 (4).
(4). и уравнений так же
и уравнений так же  свободных неизвестных, где
свободных неизвестных, где  . Если число
. Если число  , где
, где  – число линейно независимых собственных векторов, отвечающих собственному значению
– число линейно независимых собственных векторов, отвечающих собственному значению  , затем аналогично рассмотреть остальные корни
, затем аналогично рассмотреть остальные корни  кратностей
кратностей  и сложить выражения типа (3) для всех корней.
и сложить выражения типа (3) для всех корней.