
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные системы с постоянными коэффициентами и методы их решения Случай нормализуемой системы.
где
В итоге получим: (2) Система (2) распадается на n независимых ОДУ, отличающихся только правыми частями. Заметим, что каждое (достаточно гладкое) решение системы (1) (или (1одн.)) является решением системы (2) (или (2одн.)), но не наоборот. Из прошлого семестра заключаем, что общее решение системы (2одн.) имеет вид:
Лемма: Пусть  Доказательство: ◄ Подставим
Таким образом, общая схема решения системы (1одн.) изложена. Осталось ее обосновать. Для этого положим:
Рассмотрим два случая: I случай: (случай нормализуемой системы).
Поскольку Эта система каноническая и, следовательно, может быть сведена к нормальной (отсюда название “нормализуемая” система). (
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 432. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1),
(1), ,
,  – многочлен от p с постоянными коэффициентами из C. Положим
– многочлен от p с постоянными коэффициентами из C. Положим  ,
,  – порядок системы (формальный).
– порядок системы (формальный). ,
, – алгебраическое дополнение элемента
– алгебраическое дополнение элемента  .
.  – (дифференциальный оператор, а не число). “Умножим” i-ое уравнение из (1) на
– (дифференциальный оператор, а не число). “Умножим” i-ое уравнение из (1) на  слева и просуммируем по i, от 1 до n. (Если умножать элементы столбца матрицы на соответствующие алгебраические дополнения элементов того же столбца, то получим определитель матрицы, а если умножать на алгебраические дополнения другого столбца, то получим 0, на этом принципе построена обратная матрица.)
слева и просуммируем по i, от 1 до n. (Если умножать элементы столбца матрицы на соответствующие алгебраические дополнения элементов того же столбца, то получим определитель матрицы, а если умножать на алгебраические дополнения другого столбца, то получим 0, на этом принципе построена обратная матрица.) ,
,  . (В дальнейшем будет обосновано, что такое “умножение” возможно при достаточно гладких
. (В дальнейшем будет обосновано, что такое “умножение” возможно при достаточно гладких  ).
). (3), где
(3), где  – корни характеристического уравнения
– корни характеристического уравнения  , кратности
, кратности  , а
, а 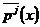 – векторный многочлен, каждая компонента которого является многочленом степени
– векторный многочлен, каждая компонента которого является многочленом степени  . Для нахождения общего решения системы (1одн.) можно было бы подставить
. Для нахождения общего решения системы (1одн.) можно было бы подставить 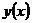 из (3) в (1одн.), найти соотношение между коэффициентами многочленов
из (3) в (1одн.), найти соотношение между коэффициентами многочленов  , выразить базисные неизвестные через свободные и обозначить эти свободные через
, выразить базисные неизвестные через свободные и обозначить эти свободные через  . Однако это слишком сложно. Для упрощения докажем лемму.
. Однако это слишком сложно. Для упрощения докажем лемму. в отдельности, что значительно проще).
в отдельности, что значительно проще).


 . Поскольку все функции
. Поскольку все функции  линейно независимы при различных k и различных
линейно независимы при различных k и различных 



 – решение системы (1одн.). ►
– решение системы (1одн.). ► + младшие степени p, некоторые
+ младшие степени p, некоторые  могут равняться нулю.
могут равняться нулю. ,
, 
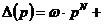
 .
. , тогда система (1) примет вид:
, тогда система (1) примет вид:
 , то есть
, то есть  .
. – замечание о гладкости решения из прошлого семестра). Так же как и в прошлом семестре в этой системе можно показать, что если
– замечание о гладкости решения из прошлого семестра). Так же как и в прошлом семестре в этой системе можно показать, что если  , то
, то  , в частности, если
, в частности, если  , то
, то 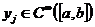 .
.