
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Квазилинейные УрЧП первого порядка. Две леммы о характеристиках.
где Геометрический смысл УрЧП (1). Пусть
Таким образом, задача нахождения всех решений класса def: Характеристической УрЧП (1) называется траектория системы ОДУ
(то есть проекция графика решения системы (2) на подпространство def: Система (2) называется системой уравнений характеристики УрЧП (1). Ее симметричная запись имеет вид:
Первая лемма о характеристиках Пусть
Тогда линия
является характеристикой УрЧП (1) Доказательство: ◄ Надо доказать только последнее равенство из (2), так как остальные равенства выполняются по условию. Имеем
так как Следствие: Если точка Доказательство: ◄ По теореме о
Вторая лемма о характеристиках Пусть  Доказательство: ◄ Пусть
так как через каждую точку поверхности проходит характеристика, |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 466. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1),
(1),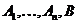 − функции от
− функции от 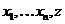 класса
класса  ,
,  , причем
, причем 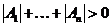
 − векторное поле в
− векторное поле в  ,
,  − решение УрЧП (1) класса
− решение УрЧП (1) класса 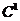 (то есть
(то есть 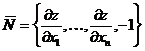 − нормаль к интегральной поверхности и УрЧП (1) имеет вид
− нормаль к интегральной поверхности и УрЧП (1) имеет вид 
 .
. (2)
(2) параллельно оси
параллельно оси  )
) .
. − решения системы
− решения системы

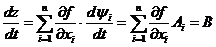 ,
, лежит на интегральной поверхности вида
лежит на интегральной поверхности вида  решения задачи Коши через точку
решения задачи Коши через точку  , далее по первой лемме о характеристиках
, далее по первой лемме о характеристиках  (в силу единственности), то есть
(в силу единственности), то есть  лежит на поверхности
лежит на поверхности  . Тогда
. Тогда ,
, 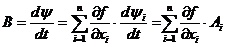 ,
, на этой поверхности
на этой поверхности  эта поверхность интегральная для УрЧП (1). ►
эта поверхность интегральная для УрЧП (1). ►