
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные однородные УрЧП первого порядка. Связь с первыми интегралами соответствующей системы ОДУ. Замечание о квазилинейных уравнениях.
Рассмотрим систему ОДУ
В прежних предположениях ( Пусть
Поскольку через каждую точку из
это линейное однородное УрЧП первого порядка относительно функции
Обратное утверждение Пусть Доказательство: ◄ Надо проверить только условие 3). Пусть
так как Лемма:
Доказательство: ◄ Подставим это
так как Теорема: Общее решение УрЧП (2) имеет вид
где Доказательство: ◄ Если Обратно: Пусть
при фиксированном
В силу полноты системы первых интегралов
следовательно По теореме о ранге, существует такая функция
Итак, для нахождения общего решения УрЧП (2) находят полную систему первых интегралов соответствующей систем ОДУ (1) 
Симметричная форма линейных однородных УрЧП первого порядка Рассмотрим УрЧП
где
(Роль x играет
(
Как показано раньше, для нахождения общего решения УрЧП (4) надо найти полную систему первых интегралов системы (5):
и записать общее решение в виде
где
Замечание о квазилинейных уравнениях Рассмотрим УрЧП
где УрЧП (6) − квазилинейное УрЧП первого порядка, оно линейно по
где Получим уравнение для Пусть
Подставим это в (6) и умножим на
Это УрЧП вида (4) для То есть
и записывают общее решение УрЧП (6) в виде (7)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 466. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1).
(1). и
и  непрерывны на
непрерывны на  ).
). − первый интеграл системы (1), тогда
− первый интеграл системы (1), тогда

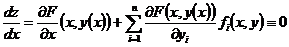
 .
. (2)
(2) .
. ,
,  ни в какой окрестности произвольной точки из
ни в какой окрестности произвольной точки из 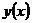 − решение системы (1), тогда
− решение системы (1), тогда ,
,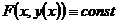 ►
►
 − первые интегралы системы (1) в области
− первые интегралы системы (1) в области  − производная функция класса
− производная функция класса 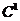 с соответствующей областью определения. Тогда
с соответствующей областью определения. Тогда  − решение УрЧП (2).
− решение УрЧП (2). в (2). Имеем
в (2). Имеем =
=  ,
, удовлетворяет условию (2) (мы с этого начинали) ►
удовлетворяет условию (2) (мы с этого начинали) ► (3),
(3), − произвольная функция класса
− произвольная функция класса  − произвольное решение УрЧП (2). Покажем, что оно представимо по формуле (3). Имеем
− произвольное решение УрЧП (2). Покажем, что оно представимо по формуле (3). Имеем
 эта алгебраическая система имеет ненулевое решение
эта алгебраическая система имеет ненулевое решение  . Следовательно ее определитель
. Следовательно ее определитель .
. всюду в
всюду в  .
. :
:  (локально) ►
(локально) ► , где
, где  , (4)
, (4) − функции класса
− функции класса  . Допустим, что
. Допустим, что  в некоторой окрестности. Разделим на
в некоторой окрестности. Разделим на  :
: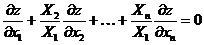 − это УрЧП вида (2)
− это УрЧП вида (2) , роль
, роль  играет
играет  , …, роль
, …, роль  играет
играет  ). Соответствующая система ОДУ имеет вид:
). Соответствующая система ОДУ имеет вид: или
или  (5)
(5) уравнение) в симметричной форме.
уравнение) в симметричной форме.

 ,
, − произвольная функция класса
− произвольная функция класса  (6),
(6), − функция класса
− функция класса  .
. , причем
, причем  (7),
(7), − функция класса
− функция класса  всюду в рассматриваемой области.
всюду в рассматриваемой области. − решение УрЧП (6), подставим это
− решение УрЧП (6), подставим это  в (7) и продифференцируем по
в (7) и продифференцируем по  :
: , (
, (  )
)  .
. , получим
, получим

 уравнений.
уравнений.
 ,
,