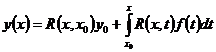Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Резольвента линейной системы ОДУ и ее свойства.def: Резольвентой системы (2) называют отображение 1) 2) Свойства: 1°
2° Пусть Доказательство: ◄ Имеем
причем
3° Доказательство: ◄ Пусть
4°
5° Доказательство: ◄
Построение линейной, однородной системы по известной ФСР. Формула Лиувилля.
Теорема: Пусть Доказательство: ◄ Рассмотрим систему
Это система вида (2) (надо разложить по первому столбцу)
где Единственность. Пусть
Умножаем справа на Формула Лиувиля.
Пусть 
так как при
Нахождение частного решения линейной неоднородной системы ОДУ методом вариации постоянных. Формула Коши.
Рассмотрим систему:
Будем искать частное решение системы (1) в виде:
где
(
Итак, решение задачи Коши
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 510. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
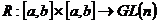 – множество невырожденных матриц порядка n, удовлетворяющих следующим условиям:
– множество невырожденных матриц порядка n, удовлетворяющих следующим условиям: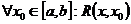 – ФМР системы (2),
– ФМР системы (2),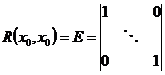 .
.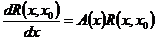 – следует из определения.
– следует из определения.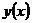 – решение системы (2) с начальными условием
– решение системы (2) с начальными условием  , тогда
, тогда 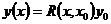 .
.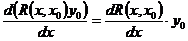
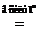
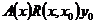 – решение системы (2),
– решение системы (2),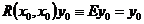 . По теореме о единственности задачи Коши
. По теореме о единственности задачи Коши 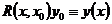 на
на 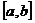 . ►
. ►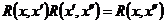 (полугрупповое свойство)
(полугрупповое свойство) – произвольный вектор из
– произвольный вектор из 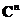 , тогда
, тогда 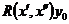 – значение в точке
– значение в точке 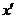 того решения системы (2), которое в точке
того решения системы (2), которое в точке 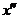 равно
равно 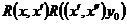 – значения точки x того решения, которое в
– значения точки x того решения, которое в 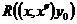 – значение в точке x того решения, которое в точке
– значение в точке x того решения, которое в точке 
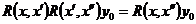 , в силу произвольного
, в силу произвольного 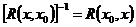 . Это следует из 3°, так как
. Это следует из 3°, так как 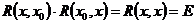 (свойство 3°). Слева аналогично.
(свойство 3°). Слева аналогично.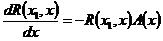
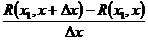 =
= 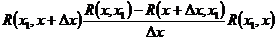 =
= 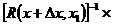
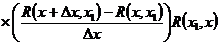
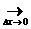
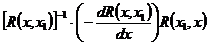 =
= 
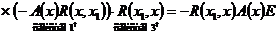 ►
►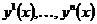 – произвольные n-мерные векторы-функции класса
– произвольные n-мерные векторы-функции класса 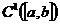 , причем
, причем 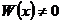
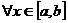 , тогда
, тогда  система вида (2), для которой
система вида (2), для которой 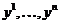 являются ФСР.
являются ФСР.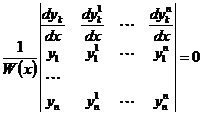 ,
, 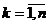 .
.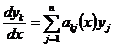 ,
,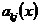 – известные непрерывные функции на
– известные непрерывные функции на 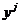 вместо y получаем два одинаковых столбца).►
вместо y получаем два одинаковых столбца).►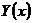 – ФМР системы
– ФМР системы 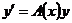 и
и 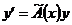 . Тогда
. Тогда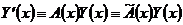 .
.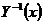 (
( 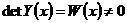
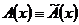 на
на 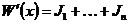 , где
, где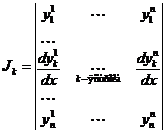 =
= 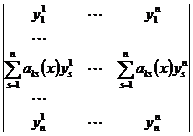
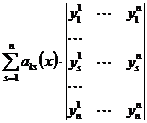 =
= 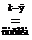
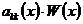 ,
,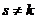 получаем две одинаковые строки
получаем две одинаковые строки 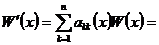
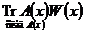
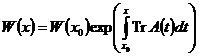 – Формула Лиувиля.
– Формула Лиувиля.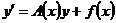 (1)
(1)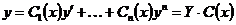 (3)
(3)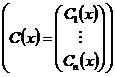 ,
,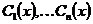 – функции класса
– функции класса 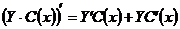
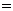
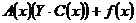
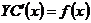
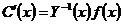
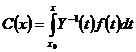
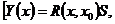
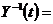
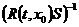
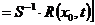
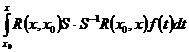
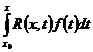 .
.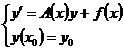 имеет вид:
имеет вид: