
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейная зависимость и независимость вектор-функций. Определитель Вронского.
Будем предполагать, что матрица
def: Система векторов
def: Система векторов-функций def: Пусть
называется определителем Вронского для векторной функции
Теорема 1: Пусть Доказательство: ◄ По условию Замечание: Обратное не верно. Пример: Теорема 2: Пусть Доказательство: ◄ Поскольку Следствие: Пусть Доказательство: ◄ Допустим, что это не так, то есть
Фундаментальная система решений (ФСР) для линейной однородной системы ОДУ. Существование ФСР и их взаимосвязь. Общее решение линейной однородной неоднородной системы.
def: Линейно независимая система решений 
называется фундаментальной матрицей решений (ФМР) системы (2). Теорема: ФСР системы (2) существуют. Их бесконечно много. Все они могут быть получены из одной по формуле Доказательство: ◄ Фиксируем произвольную точку
то есть
По теореме о единственности решения задачи Коши (для каждого столбца) получим
Теорема: Общее решение системы (2) имеет вид Доказательство: ◄ ( (
имеет единственное решение
Теорема: Общее решение неоднородной линейной системы (1)
где
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 777. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
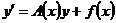 (1)
(1)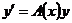 (2) – соответствующая однородная система.
(2) – соответствующая однородная система. и
и  непрерывны на
непрерывны на 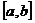 со значениями в С.
со значениями в С.
 на
на  ,
,  такие, что
такие, что 
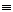
 .
. на
на  на
на  .
.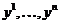 – n - мерный вектор функции на
– n - мерный вектор функции на 
 .
.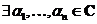 ,
,  ,
, 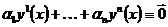

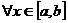 столбцы
столбцы  линейно зависимы
линейно зависимы  , тогда
, тогда  и
и  линейно независимы на
линейно независимы на  . Действительно пусть
. Действительно пусть 


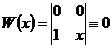 на
на  такая, что
такая, что  , тогда
, тогда  линейно зависимы, то есть
линейно зависимы, то есть  . Положим
. Положим  , тогда
, тогда  – решение системы (2) в силу ее линейности и однородности. Далее
– решение системы (2) в силу ее линейности и однородности. Далее 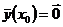 по построению заметим, что
по построению заметим, что  так же решение системы (2) с теми же начальными условиями. По теореме о единственности решения задачи Коши
так же решение системы (2) с теми же начальными условиями. По теореме о единственности решения задачи Коши 
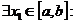
 , тогда
, тогда 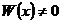

 . По Теореме 2 тогда
. По Теореме 2 тогда  , а это противоречит условию. ►
, а это противоречит условию. ►
 , где
, где 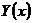 – фиксированная ФМР, а S – матрица
– фиксированная ФМР, а S – матрица  , с условием
, с условием  .
. . Пусть B – матрица
. Пусть B – матрица 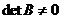 , тогда по теореме о
, тогда по теореме о  решения задачи Коши
решения задачи Коши 
 системы (2) (
системы (2) (  . В этом случае
. В этом случае  , поскольку матриц B с условием
, поскольку матриц B с условием  – произвольная ФМР системы (2). Положим
– произвольная ФМР системы (2). Положим  , тогда
, тогда

 ,
, – матрица из решений системы (2), причем
– матрица из решений системы (2), причем =
=  =
=  =
=  .
. на
на  (3), где
(3), где  – произвольные постоянные (из C).
– произвольные постоянные (из C).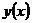 из формулы (3) является решением системы (2) в силу ее линейности и однородности.
из формулы (3) является решением системы (2) в силу ее линейности и однородности. ) Пусть
) Пусть  – произвольное решение системы (2), а
– произвольное решение системы (2), а 
 , то есть ее определитель равен
, то есть ее определитель равен  . Положим
. Положим  , тогда
, тогда  по построению. По теореме о единственности решения задачи Коши
по построению. По теореме о единственности решения задачи Коши  на
на  . ►
. ►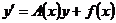 имеет вид:
имеет вид: ,
,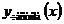 – частное решение системы (1),
– частное решение системы (1),