
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лемма о равномерной непрерывности.def: Метрическое пространство называется компактом, если из каждого покрытия его открытыми множествами (открытое покрытие) можно выделить конечное подпокрытие. Лемма: Пусть Доказательство: ◄ Выберем произвольно Пусть
Так как:
Непрерывность решения системы ОДУ по начальным данным и параметру. Теорема: Пусть
Доказательство: ◄ 1) Допустим, что это не так. Тогда По теореме Больцано-Вейерштрассе:
так как  Поскольку 2) Пусть Сделаем оценки:
и вычитаем из одного другое:
(заметим, что
(По замечанию к лемме Гронуолла)
(не зависит от x и при достаточно малых Продолжим
В силу Из первой части
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 474. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 – метрические пространства,
– метрические пространства,  – метрический компакт, а
– метрический компакт, а  – непрерывно на всем
– непрерывно на всем 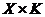 , тогда
, тогда  – непрерывно по
– непрерывно по  и эта непрерывность равномерна по
и эта непрерывность равномерна по  , то есть
, то есть  и
и 
 , что
, что 
 ,
,  выполняется неравенство
выполняется неравенство  (то есть
(то есть  не зависит от k).
не зависит от k). и
и  . Надо найти
. Надо найти  . В силу непрерывности
. В силу непрерывности  в точке
в точке  имеем
имеем 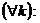




 . Используя аксиому выбора можно считать, что задана функция
. Используя аксиому выбора можно считать, что задана функция 
 на всем К. Заметим:
на всем К. Заметим:  , где
, где 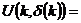
 – открытый шар в К, с центром в точке k, радиуса
– открытый шар в К, с центром в точке k, радиуса 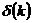 . В силу компактности К, имеем
. В силу компактности К, имеем 
 :
:  . Положим
. Положим  , тогда
, тогда  ,
,  ,
, 
 , то есть
, то есть  . Имеем:
. Имеем: +
+  .
. – для первого слагаемого,
– для первого слагаемого, – для второго слагаемого. ►
– для второго слагаемого. ► – метрическое пространство,
– метрическое пространство,  – открытое множество в
– открытое множество в  , функция
, функция  – непрерывна на
– непрерывна на  , удовлетворяет условию Липшица по у. Далее: пусть
, удовлетворяет условию Липшица по у. Далее: пусть 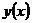 – решение задачи Коши:
– решение задачи Коши:  , при
, при  ,
,  и
и  , определенное на
, определенное на 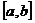 . Тогда
. Тогда  , что
, что  =
= 
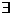 ! решение
! решение  задачи (1), (2), определенное на всем
задачи (1), (2), определенное на всем  , и эта непрерывность равномерна по
, и эта непрерывность равномерна по  , то есть
, то есть  ,
,  ,
, 


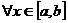 ,
,  ,
, 
 ,
, 
 .
.
 ,
,  ,
,  ,
,  ,
, 
 .
. . Заметим, что
. Заметим, что


 ,
, . В этом случае
. В этом случае  , так как
, так как 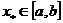 ,
,  и точку
и точку  можно считать аргументом
можно считать аргументом  определено на
определено на 
 – имеет смысл
– имеет смысл  . В силу открытости D, точка
. В силу открытости D, точка  , при достаточно больших k, а это противоречит выбору точек
, при достаточно больших k, а это противоречит выбору точек 
 .
. ,
,  ,
,  :
:  &
&  это следует из открытости множества, непрерывности
это следует из открытости множества, непрерывности 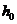 и условия
и условия  . Выберем
. Выберем  ,
,  .
. , тогда точка
, тогда точка  задачи Коши (1), (2), определенное в окрестности точки h. Заметим так же, что
задачи Коши (1), (2), определенное в окрестности точки h. Заметим так же, что 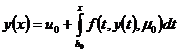 =
=  +
+  ,
, 

 +
+ 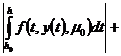
 + +
+ + 
 +
+  + +
+ + 
 определено при всех
определено при всех  и
и 
 );
);  ,
,  ; по лемме о равномерной непрерывности:
; по лемме о равномерной непрерывности:  при
при  равномерно по
равномерно по  при
при  )
)





 выйдет на границу
выйдет на границу  только при
только при  и
и 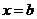 .
. непрерывно по
непрерывно по  , равномерно по
, равномерно по  . Проводя для
. Проводя для